| Childlessness and Genetic Relatedness. Their Influence on Sibling Ties in a Post-Industrial Society. (Thomas Pollet) |
| home | list theses | contence | previous | next |
In this thesis we examine the effects of childlessness and genetic relatedness on sibling relationships. In this introduction we briefly outline the structure of this project.
Recently, it has been argued that individualization processes have thoroughly altered family relationships. First, we will very briefly discuss these sociological perspectives on modernization and individualization (2.1). The core idea is that traditional institutions, e.g. marriage, are being replaced by ‘individualized choice’. Moreover according to this perspective, social relationships become centred upon choice. Therefore (traditional) family ties are expected to dissolve. One of the consequences of individualization is the increasing rates of below-replacement fertility and (voluntary) childlessness observed in Western countries. Under 2.2, we will review findings on (voluntary) childlessness and concomitant characteristics.
We will then discuss biological perspectives on kin selection and human behaviour (3). Following this perspective, we derive that childless individuals are likely to maintain stronger relationships with their siblings than ‘parents’. Such high quality relationships could have inclusive fitness consequences. Relationships between full siblings are also predicted to be better than between half-siblings, or relationships where the siblings are unrelated.
Furthermore, we will briefly discuss how social factors affect relationship quality, from a (micro)sociological point of view (4). This is important as we want to examine the effects of childlessness and genetic relatedness on relationship quality, while controlling for other social factors affecting the sibling relationship, e.g. the financial balance of the relationship.
Using a dataset on kinship relations in the Netherlands, the Netherlands Kinship Panel Study, we will then empirically investigate the effects of childlessness and genetic relatedness on sibling relationships. In the first part of the analysis we will assess the effects of childlessness and genetic relatedness on relationship quality (7.1 to 7.3). In the second part of the analysis, we examine the influence of childlessness and genetic relatedness on other relationship aspects, i.e. investment measures (7.4). Finally we will examine differences in sibling relationship characteristics between the voluntary childless and the involuntary childless (7.5).
Due to considerations of length, additional statistical information and coding procedures can be found on the cd-rom. In addition, due to the number and extent of the analyses, we will only discuss the most relevant results of our analyses, i.e. the effects of childlessness and genetic relatedness, rather than all results. Throughout this thesis we will use five percent as significance level.
2. Individualization, childlessness and social relations
2.1 Individualization
“The general diagnosis is that people’s lives are becoming more mobile, more porous, and of course more fragile. In the place of pre-given and often compulsory types of relationship is appearing the ‘until the next thing’ principle, as Bauman calls it, a kind of refusal of lifelong plans, permanent ties, immutable identities. . . . Instead of fixed forms, more individual choices, more beginnings and more farewells.” (Beck-Gernsheim, 2002: 41)
Society has changed drastically over time and rapid modernization has drastically altered contemporary society. According to several social theorists, e.g. Giddens (1991), these modernization processes have led to the breakdown of traditional institutions (e.g. marriage) in late modern societies. Whereas ‘traditional society’ was characterized by institutions and social structures that guided individuals from birth to death, radicalized modern societies have become more and more centred upon ‘individual choice’ (Giddens, 1991; Beck, 1993; Beck & Beck-Gernsheim, 2002). What is left of traditional institutions and norms will further disappear and make way for individualized choice. In late modern societies, individuals have more opportunities for self-expression but also have more uncertainty. Life in late modern societies has become a quest for identity, with all the perils such quests entail.
Individuals are now forced to choose with whom they maintain social relationships as well as to construct their own identities, whereas in traditional society this was governed by traditional norms and social institutions (Giddens, 1991; Beck, 1993; Beck & Beck-Gernsheim, 2002). Rather than relying on traditional institutions as sources for ‘identity scripts’, individuals in radicalized modern societies are confronted with a wide variety of choices for their identity construction. Individual ‘narratives’, life stories, have become more flexible and open-ended. In the absence of institutional solutions, social relationships, including family relationships, have become increasingly open to negotiation and subject to ‘termination’ (Beck, 1993).
2.2 Childlessness and concomitant characteristics
It is ‘individualized choice’, guided by the changed costs and benefits of children (Becker, 1991), that (partially) explains the below-replacement fertility patterns observed in Western countries today (Morgan & King, 2001).[1] The choice to become a parent in a radicalized modern society requires long-lasting financial and emotional investment (van de Kaa, 2004). Individuals can choose not to make such a commitment and not to have a (or another) child. Thus, in radicalized modern societies, because of the availability of contraception, individuals are ‘free’ to choose how many children they have, or whether they have any children at all (McAllister & Clarke, 1998; van de Kaa, 2004).[2] Research has shown that there is an increasing trend of individuals who choose to be childless in radicalized modern societies (DeOllos & Kapinus, 2002; Park, 2005). For the United States, estimates are that approximately seventeen percent of the women born between 1944 and 1955 and up to twenty-two percent of the women born between 1956 and 1972 will remain childless (DeOllos & Kapinus, 2002).[3] The majority of these women are supposedly voluntary childless (Gillespie, 2003; Park, 2005; see McAllister & Clarke, 1998). Similar estimates exist for the UK and the Netherlands, but there is some variation across European countries (NIDI, 1997/2004; McAllister & Clarke, 1998; Ruddock et al., 1998; Pearce et al., 1999). These increasing rates of voluntary childlessness are predominantly a Western phenomenon (Gillespie, 2003). In many other parts of the world contraceptives and reproductive technologies, which facilitate the choice of (voluntary) childlessness, are still largely unavailable. It should also be noted that data on (voluntary) childlessness in men are scarce (McAllister & Clarke, 1998).
Compared with ‘mothers’, voluntary childless women are more likely to be higher educated and employed (McAllister & Clarke, 1998; Bachu, 1999), have a managerial job (McAllister & Clarke, 1998; Bachu, 1999), less religious (Mosher et al., 1992), less traditionally gender orientated (Callan, 1986) and less conventional (Park, 2005). It is unclear, however, whether there is a difference in life satisfaction between ‘parents’ and childfree individuals (Magarick & Brown, 1981; Callan, 1986; Somers, 1993). However, childless couples tend to report higher marital satisfaction than ‘parents’ (Callan, 1987; Somers, 1993). Although, Somers (1993) found no effect of childlessness on marital satisfaction after controlling for religious affiliation and income. While childless couples report higher marital satisfaction than parents, they believe their friends and relatives view them negatively because of their (voluntary) childlessness (Somers, 1993). In late modern societies, childless individuals, especially women, are also often stigmatized (Campbell, 1985; Park, 2002/2005).
According to individualization theory, the increasing rates of below-replacement fertility and (voluntary) childlessness can be explained by ‘choice’ (van de Kaa, 2004). Individuals who choose to remain childless can allocate their time and money in a different way and devote these available resources to self-expression (see Giddens, 1991).
If individuals do not have children, whether they choose to or not, they can allocate their time and money in a different way. Childless individuals can choose to maintain other strong relationships which they perceive as important as having children. Childless individuals do not face the trade-off between ‘investment’ in their children and ‘investment’ in their other social relationships. This could in part explain the finding that childless couples are more satisfied with their marriage than parents (Somers, 1993).
Following individualization theory, whether or not social relationships, including kin relationships, are of high quality has become increasingly dependent on choice. Therefore, whether or not childless individuals maintain good relationships with their siblings is (solely) a matter of individualized choice. If (traditional) family ties dissolve in radicalized modern societies, as individualization theory argues (Giddens, 1991; Beck-Gernsheim, 2002), nothing prohibits childless individuals from maintaining high quality relationships with their partners or friends instead of with their siblings. Childless individuals could invest more time and money in relationships with their partner and/or friends, instead of with their siblings. So, following individualization theory, there is no apparent reason why childless individuals should (continue to) invest in the relationship with their sibling, other than choice. Childless individuals could choose to invest in their relationship with their partner or friends instead. There is possible evidence that childless individuals do so, i.e. their higher marital satisfaction (Callan, 1987; Somers, 1993).
However, from an inclusive fitness point we might expect that childless individuals do maintain ‘strong’ relationships with their (full) siblings, as we will discuss in the following section. These relationships bring along costs in time and money. Maintaining such strong relationships, which require investments in terms of time and money, could be adaptive, at least to a certain extent, and could generate some inclusive benefits for childless individuals. It could be an example of human adaptive decision making, even in radicalized modern societies.
Moreover, if according to individualization theory, family relationships become increasingly centred upon individualized choice rather than (traditional) norms or institutions, we would not expect strong differences in sibling relationships according to genetic relatedness. If choice becomes the crucial determinant of family relationships, genetic relatedness should only play a minor role in sibling relationships and their characteristics. From an inclusive fitness point of view, however, sibling relationships are expected to vary in quality, for instance, according to genetic relatedness.
3. Inclusive fitness and adaptive decision making
Hamilton (1964) developed the concept of inclusive fitness, which can be defined as “the sum of direct and indirect fitness” (Alcock, 1998: G2). Direct fitness refers to genes contributed to the following generation by an individual through personal reproduction, whereas indirect fitness refers to genes contributed in the next generation by helping (non-descendant) relatives. As shown for insect societies (Wilson, 2000[1975]), an individual’s apparent altruistic behaviour can in certain cases be explained by Hamilton’s Rule (r*b>c). For humans, this implies that, under circumstances, it is beneficial to behave altruistically towards (closely) related kin as this might increase their inclusive fitness. There is evidence that kin selection has played a crucial role in shaping human behaviour and influences human behaviour even today.
Within traditional societies, kin often provide (mutual) material and immaterial support. Among the Yanomamö of Venezuela, coalitions for raids are formed based on relatedness (Chagnon & Bugos, 1979). Closer related individuals are more likely to form coalitions in raids, than distantly or unrelated individuals. Similarly, an analysis of data on Norse earldoms, Icelandic families and English royalty, showed that relatedness influences the likelihood of (mutual) support and lethal conflict (Johnson & Johnson, 1991). Support of closely related individuals was common, but fatal conflict between closely related individuals was highly unlikely. An analysis of Viking sagas showed similar results (Dunbar, Clark & Hurst, 1995). In these sagas, closely related kin were found to form more stable, unconditional alliances than distantly related or unrelated individuals.
Besides forming coalitions for conflict, closely related kin often cooperate to overcome what is known as ‘the dilemma of collective action’ (Olson, 1965). For instance, among the Ye’kwana of Venezuela (Hames, 1987) and the K’ekchi of Belize (Berté, 1988), kin help each other with agricultural tasks without requiring a direct return for the given help from their relative. By contrast, help from unrelated individuals appears to be based on direct reciprocity. Among the Inuit, cooperative hunting groups are formed based on relatedness (Morgan, 1979; but see Alvard, 2003). For traditional societies, it has also been shown that closely related kin often share meat as well as other food items (Cashdan, 1985; Betzig & Turke, 1986; Gurven et al., 2000; Gurven, 2004). Similarly, an analysis of worker remittances showed that closely related kin are more likely to receive money than distantly related kin (Bowles & Posel, 2005).
Kinship cues, sharing the same last name, have also been shown to facilitate altruism (Oates & Wilson, 2002). In addition, individuals appear more willing to incur significant ‘costs’ for closely related individuals than for distantly related or unrelated individuals (Burnstein et al., 1994; Barrett et al., 2002: 49-ff). Incurring costs to aid closely related kin, rather than distantly related or unrelated individuals, is also more likely to be deemed rational and ethical (Kruger, 2001).
Kin also make up a significant proportion of one’s social network (Dunbar & Spoors, 1995; Hill & Dunbar, 2003). Furthermore, in traditional societies closer related individuals been shown to interact more often with each other than distantly related kin (Hames, 1979). In (radicalized) modern societies, genetic relatedness is a significant predictor of subjective closeness and social support (Neyer & Lang, 2003). The important role of kin for social support, e.g. Miller and Darlington (2002) and Kana'Iaupuni and colleagues (2005), could lead to significant inclusive benefits, even in modern societies.[4]
The presence and help of related individuals can even be crucial for survival. For instance, McCullough and Barton (1991) found that relatedness affected survivorship of the Mayflower disaster. In a similar way did an analysis of the Donner Party disaster show that relatedness influenced survival chances and longevity of individuals (Grayson, 1993 in Barrett et al., 2002: 64-65). For traditional societies, it has been shown that the presence of (matrilineal) kin, especially grandmothers, lowers the risk of infant mortality (Hawkes et al., 1997; Sear et al., 2000/2002 but see Adams et al., 2002). The role of kin for survival of children was also clear in the analysis of the Mayflower disaster (McCullough & Barton, 1991). If children had one parent who survived the winter at the Plymouth colony, they (all) survived.
In modern societies, genetic relatedness has been shown to affect the occurrence of child abuse. Rates of child abuse, and fatal child abuse, are significantly lower in households where both parents are related to the child (Daly & Wilson, 1981/1985/1988). Moreover, genetic relatedness influences the occurrence of murder. In modern societies, the occurrence of murder between (closely) related individuals appears to be relatively low (Daly & Wilson, 1982/1988).
(Female) Kin also often provide childcare and their help can increase an individual’s inclusive fitness (Turke, 1988/1989; Bereczkei, 1998; Sear et al., 2000/2002). Such ‘helper’ behaviour between related individuals has been shown in several non-human species (Kurland, 1980; Emlen, 1995). In humans, kin can also serve as ‘helper’s at the nest’ and individuals of low reproductive value, e.g. grandmothers, often help kin (Hawkes et al., 1997; Sear et al. 2000). The presence of (matrilineal) kin has been shown to have significant beneficial effects on infant survival and (inclusive) fitness (Hawkes et al., 1997; Sear et al., 2000/2002 but see Adams et al., 2002). In traditional societies, older siblings also often fulfil a ‘helper role’ (Weisner & Gallimore, 1977; but see Crognier et al., 2001). Older siblings can take care of younger siblings, while the mother is occupied with domestic labour and/or provisioning. For instance, among the Toba of Argentina, girl helpers were shown to significantly reduce the workload of the mother by helping and caretaking (Bove et al., 2002; but see Hames & Draper, 2004). Caretaking by elder siblings could have beneficial effects on younger siblings’ their development (Sigman et al., 1988; see Belsky et al., 1991). In modern societies, childless individuals could fulfil helper roles, as suggested by Essock-Vitale and McGuire (1985).
The absence of helping kin has been cited as a critical factor for the demographic transition by Turke (1989). Turke (1989) argued that the emergence of the nuclear family and the breakdown of extended kin networks as key factors for the demographic transition. These processes have shifted the burden of children to increasingly smaller families. Therefore, in the face of increasing costs and low benefits, individuals nowadays choose to have less children or have no children at all (Morgan & King, 2001; van de Kaa, 2004). As we have discussed above, individuals who do not have children can allocate the time and money, which they would otherwise invest in children, differently.
Although, helping behaviour between kin is common, as described above, several studies have shown that evolution can promote intense competition between kin as well, especially sibling rivalry (Mock & Parker, 1997/1998). Sibling rivalry occurs in several animal taxa (birds: O’Connor, 1978; insects: Grbic et al., 1992; mammals: Frank et al., 1991; Cockburn, 1994) and even in plants (Shaanker et al., 1988).
For humans, it has been shown that if births are closely spaced, survival rates tend to decline for children (Hobcraft et al., 1985; Curtis et al., 1993; Alam, 1995). This could be attributed to sibling rivalry for parental investment. For example, Muhuri and Preston (1991) showed that girls in Bangladesh have a higher mortality risk, if they have an elder sister. Boys were found to have a higher mortality risk, if they have two older brothers (Muhuri & Menken, 1997). There was also an increase in mortality risk, indifferent of sex, if the first born was a son. Apart from affecting infant mortality, sibling rivalry has been argued to have significant effects on psychological development (Sulloway, 1996/2001).
Besides the occurrence of strong competition between kin, it should also be taken into account that decisions on whether or not to support kin are contingent upon several other factors. As with all individual decision making in a social context (Parsons, 1937; Coleman, 1990), an individual’s decision to ‘invest’ in kin relations depends upon a wide variety of factors. For instance, Wang (1996) found that besides genetic relatedness, other factors, e.g. age, influenced risk-sensitive decision making. In his experiment subjects were asked to choose between a deterministic option and a probabilistic option to ‘save’ related individuals. Besides relatedness, decision making was found to be influenced by age, gender and social context. Likewise, Dunbar, Clark and Hurst (1995), in their study of Viking sagas, found that besides relatedness, other factors, such as perceived dangerousness, influenced decisions whether or not to avenge a murder of a related individual or settle for blood money.
Of special importance for kin-based decision making is the factor ‘reproductive value’ (Hughes, 1988). Reproductive value refers to the probable number of offspring an individual will have during the rest of his or her lifetime (Low, 2000: 64; Barrett et al., 2002: 52). This concept, first developed by Fisher (1958 [1930]), has been utilized for a wide variety of demographical issues, e.g. Keyfitz (1977), but also has implications for the analysis of human kin-based decision making. Wang’s (1996) experiment shows that respondents take into account reproductive value while making risk-sensitive decisions. If the reproductive value of the related individuals was low, respondents were more likely to choose the probabilistic option over the deterministic option. If the reproductive value of respondents was high, respondents were much more likely to choose a deterministic option. Respondents were thus more likely to ‘gamble’ with decisions affecting individuals with low reproductive value than with individuals who have high reproductive value. Bowles and Posel (2005) also found that reproductive value influenced kin-based decision making. Relatedness weighted for reproductive value, explained more of the variance in migrant workers’ remittances to their family than genetic relatedness in itself. When deciding how to allocate their remittances migrant workers take into account reproductive value, as well as other factors, e.g. economic need, besides genetic relatedness.
The literature on kin selection and human decision making readily shows that, under circumstances, individuals help their (closely related) kin, leading to a higher inclusive fitness. In our opinion, childless individuals also make this type of adaptive decisions, at least to a certain extent. Childless individuals can choose to invest their time and money in relations with their friends, partner(s) or kin. As they do not ‘invest’ in offspring they are able to allocate their time and money differently, towards their relationship(s) with their partner, kin and friends. As already discussed, based on individualization theory, there is no apparent reason why childless individuals should choose to maintain a stronger relationship with their siblings than parents.
However, from an inclusive fitness point of view, childlessness, whether by choice or not, should affect the relationship with an individual’s kin. As childless individuals do not have to trade off investments between their relationship with kin and with their offspring, they are predicted to have ‘better’ relationships with their kin than ‘parents’, all else being equal. Such stronger relationships could have inclusive fitness consequences. As we will discuss in the following section, high quality relationships are likely to go together with investments.
There is some evidence that childless individuals invest more in relationships with their kin. Essock-Vitale & McGuire (1985) found that childless women were significantly more likely than ‘parents’ to give help to their nieces and nephews. Yet, childless women were also found more likely to receive help from their nieces and nephews. Nelson (1998) found that childless women were more likely than parents to support nieces and nephews and siblings. However, the effects of childlessness on sibling relationships have not been thoroughly studied from an evolutionary perspective, while controlling for other factors that influence relationship characteristics.
Besides childlessness, relatedness is of importance for this study. Closer related individuals should generally have stronger relationships than distantly related or unrelated individuals. Therefore relationships between full siblings (r=0,5) are predicted to be stronger than between half-siblings (r= 0,25) or relationships where a sibling is adopted (r= 0). Moreover, relatedness is predicted to influence social and financial investment in sibling relationships. Relationships between closer related individuals are predicted to show more investment than those of distantly related individuals, all else being equal.
4. Social factors and quality of relationship
‘Birds of a feather flock together’
As our analyses mainly focus on quality of social relationships, we will briefly discuss social factors affecting quality of relationship using insights from (micro)sociology.
According to the exchange paradigm (Homans, 1951/1958; Blau, 1964; for a review: Cook & Whitmeyer, 1992), social relationships can be seen as forms of immaterial and/or material exchange. Gift or money relationships will, to a certain extent, reflect the strength of a dyadic relationship. Symmetrical money or gift-giving relationships, rather than asymmetrical relationships, for instance, are likely to be a reflection of a high quality relationship. Similarly, relationships in which individuals show equal social investment, e.g. contacting each other, are predicted to be of a higher quality. In general, ‘symmetrical’ relationships are predicted to be more stable and of a higher quality. Power asymmetries are likely to be unstable and lead to a negative evaluation of a dyadic relationship (Blau, 1964 but see Molm, 1997).
Structural sociological theory predicts that social relations between individuals are structured by the characteristics they share, also referred to as ‘homophily’ (Blau, 1977/1980; McPherson et al., 2001). Within a certain dyad, the degree of ‘homophily’ is a strong predictor of the strength and quality of a dyadic relationship. Therefore, for example, if age differences between siblings are large their relationship is expected to be of a poorer quality.
Research on social support has shown that women rely more on their relatives than men for emotional and social support (Turner & Marino, 1994; Phillipson, 1997). In contrast, men tend to primarily rely on their partner for social and emotional support (Turner & Turner, 1999; Mirowsky & Ross, 2002). Therefore, we expect that women have better relationships with their siblings than men.
From a social network perspective (McPherson et al., 2001), it is important to bear in mind that high quality social relationships, strong ties, often require ‘high (mutual) investments’ in terms of time and money.[5] Humans, like other primates, appear inherently limited in the number of these strong, high quality relationships they have (Dunbar, 2004 [1996]). These high quality relationships are part of a vertically structured network, with distinct groupings, e.g. ‘support cliques’ and ‘sympathy groups’ (Hill & Dunbar, 2003; Zhou et al., 2005).
Support cliques can be described as the set of individuals with whom one maintains ‘strong’ relationships as well as turns to for advice or support while under financial or emotional distress (Dunbar & Spoors, 1995; Hill & Dunbar, 2003). Support cliques generally consist of three to five individuals. The support clique size appears to be fairly constant across cultures and has been replicated in several studies (Marsden, 1987; Dunbar & Spoors, 1995; Dunbar, 1998). Whereas support cliques seem to typically consist of about three to five individuals, (human) sympathy groups consist of approximately twelve individuals (Buys & Larsen, 1979; Dunbar, 1993/1998/2004; Dunbar & Spoors, 1995; Hill & Dunbar, 2003). These individuals are typically contacted once a month. Based on extrapolation of primate data on group size and relative neocortex size, the overall size of an individual’s social network is predicted to be limited to approximately 150 individuals (Dunbar, 1993). Cross-cultural evidence, sociological and organizational studies, e.g. Coon (1946), support this prediction (Dunbar, 1993/2004).
Given the findings of a fairly constant size of support cliques and human sympathy groups, the number of high quality relationships is inherently limited. This implies that the relationship quality of one relationship is traded off against other relationships. As childless individuals do not have to trade off high quality relationships with relationships with their children, they are predicted to have higher quality relationships with their siblings than parents.
5. Research questions and aims of the study
The main research question of this project is whether or not childless individuals maintain stronger relationships with their sibling than ‘parents’ (7.1). Genetic relatedness is also expected to significantly influence relationship quality. If we would find differences according to these variables this leads to suspect that kin selection might play a role, contrary to the claim that family relationships have become centralized (solely) upon ‘individualized choice’. Furthermore, we will investigate whether these high quality relationships require ‘symmetry’ and ‘investment’. By investment we refer to investment in terms of time (showing interest, showing initiative to contact the other) and money (donating or lending).
This study will investigate the effects of childlessness and genetic relatedness on relationship quality with a sibling whilst controlling for ‘investments’ as well as other aspects influencing the relationship, e.g. differences in age between the siblings. Therefore we will follow a multivariate design, which allows examining the independent effects of genetic relatedness and childlessness on relationship quality while controlling for other variables.
The effects of genetic relatedness and childlessness on other relationship aspects besides quality, i.e. ‘investments’, will then be investigated separately (7.4). For instance, childless individuals are expected to show more interest in the personal life of their sibling, but not necessary receive more interest from their sibling, than parents.
The relationship aspects which we will analyze are giving and receiving interest (7.4.1 to 7.4.3), initiative of contact (7.4.4), financial balance (7.4.5) and giving and receiving financial help (7.4.6 to 7.4.8). The effects of childlessness and genetic relatedness will be examined on these relationship aspects while controlling for the other relationships aspects. Childless individuals are predicted to invest more than parents, although they could also have symmerical relations, as symmetry is characteristic for high quality relationships. A higher degree of relatedness is predicted to lead to more investment in sibling relationships.[6]
In addition, we will investigate differences between the voluntary and the involuntary childless (7.5). This allows to examine the claim by individualization theory that the higher educated are likely to be childless by choice. Of interest is also whether involuntary childless individuals maintain stronger relationships with their sibling than ‘childfree’ individuals. Also, we will look at differences between involuntary childless and childfree individuals in terms of ‘investment’. Involuntary childless individuals are predicted to invest more in their sibling relationship than ‘childfree individuals’. If differences between the ‘childfree’ and the involuntary childless in investment or relationship quality occur, this indicates that ‘choice of childlessness’ plays a role for sibling relationships.
In conclusion, first we will investigate the effects of childlessness and genetic relatedness on the quality of the relationship, while attempting to control for other factors influencing the sibling relationship. Then we will examine whether childlessness and genetic relatedness affect other dimensions of the relationship, e.g. whether or not money or valuables are given. Finally, we will compare the childfree and involuntary childless individuals for relationship quality and other dimensions of sibling relationships.[7]
6. NKPS-Dataset and methodology
6.1 The NKPS dataset and the selected variables
The first wave of the Netherlands Kinship Panel Study (NKPS) dataset was obtained through the Netherlands Interdisciplinary Demographic Institute (NIDI). The NKPS is a large scale longitudinal study, designed to investigate family and kin relations in the Netherlands (Dykstra et al., 2004). The first wave was completed mid-2004; we used this version (version of 4-7-04; main sample). The sampling procedure, representativity as well as the survey method is described in detail by Dykstra and colleagues (2004).
In order to ensure we correctly coded childlessness, we selected all individuals of forty years or older. We assume that forty years is more or less the age at which the reproductive phase is completed. Individuals were then coded as ‘childless’, if they did not have any children by any means (including adoption), and stated that they had no intentions of having children in the future.[8] As we selected only individuals over forty, all analyses presented here are unweighted for the global Dutch population structure. Several variables were recoded, the procedure of recoding can be found on the cd-rom. In the NKPS-survey questions were asked about ‘sibling a’, a randomly selected sibling of the respondent. Correspondent characteristics, e.g. gender of sibling a, were matched, as described on the cd-rom.
The variables selected for analyses are presented in
the table below (Table 1). The correspondent questions and additional information can
be found in the NKPS codebook (Dykstra et al., 2004), except for the constructed
variables (age difference, sibling a childless;
education; sex sibling a; total living sibs; genetic status sibling a)
for which additional information, can be found on the cd-rom.
Table 2 contains additional information on the questions used for
certain variables.
Table 1 : Variables and categories
|
Variables |
Categories |
|
Sibling a childless |
0= children; 1= childless |
|
Education |
1= incomplete primary or primary |
|
|
2= lower vocational |
|
|
3= lower general secondary |
|
|
4= medium general secondary |
|
|
5= upper general secondary |
|
|
6= intermediate vocational |
|
|
7= higher vocational |
|
|
8= university or postgraduate |
|
Age difference between siblings[9] |
interval (difference birth years) |
|
Age (at interview) |
interval |
|
Sex |
0= male; 1= female |
|
Sex sibling a |
0= male; 1= female |
|
Childlessness |
0= children; 1= childless |
|
(Total) Living (full) siblings |
interval |
|
Genetic status[10] |
0= adopted or half-sibling |
|
|
1= full sibling |
|
Quality of relationship |
1= not great |
|
|
2= reasonable |
|
|
3= good |
|
|
4= very good |
|
Financial balance |
1= respondent gives more |
|
|
2= balanced |
|
|
3= other gives more |
|
Financial help given |
0= yes; 1= no |
|
Financial help received |
0= yes; 1= no |
|
Interest given |
1= not at all |
|
|
2= once or twice |
|
|
3= several times |
|
Interest received |
1= not at all |
|
|
2= once or twice |
|
|
3= several times |
|
Initiative contact |
1= usually my initiative |
|
|
2= more or less equal |
|
|
3= usually other's initiative |
|
Conflict |
1= not at all |
|
|
2= once or twice |
|
|
3= several times |
Table 2 : Formulation of questions for certain variables (Dykstra et al., 2004)
|
Education |
(Highest achieved level of education) |
|
Financial balance |
Giving and receiving is an important aspect of relationships. |
|
|
How would you describe your relation with {name, description}, |
|
|
do both of you give about the same amount, do you give more |
|
|
than the other, or does the other give more. |
|
Financial help received |
Has {name, description} given you valuable objects or a |
|
|
substantial amount of money in the past 12 months? |
|
|
Please include any monthly transfers |
|
Financial help given |
Have you donated {name, description} valuable objects or a |
|
|
substantial amount of money in the past 12 months? |
|
|
Please include any monthly transfers |
|
Interest given |
Have you shown an interest in the personal life of |
|
|
{name, description} in the last 3 months? |
|
Interest received |
Has {name, description} shown an interest in your personal life |
|
|
in the last 3 months? |
|
Quality of relationship |
Taking everything together, how would you describe your relation |
|
|
with {name, description}? |
|
Conflict |
Have you had any conflicts, strains or disagreements with |
|
|
{name, description} in the past 3 months? |
|
Initiative of contact |
When you’re in touch with {name, description}, do you usually get |
|
|
in touch at your initiative, at your partner’s initiative, or is it |
|
|
more or less equal? |
(Source: Dykstra et al. 2004)
6.2 Preliminary analyses (HOMALS)
Before we examine the effects of childlessness and genetic relatedness on quality of relationship in a multinomial logistic design, we present descriptive statistics and some exploratory analyses.
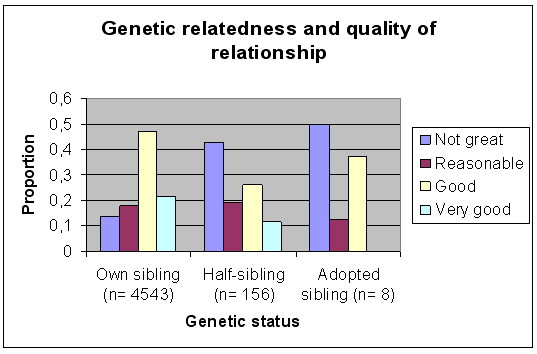
The relationship between genetic status and quality of relationship is significant (χ² = 120,24; df= 6; p= 1,45*10-23; Figure 1).[11] As there are only a small number of cases where sibling a was adopted, we merged the categories ‘half-sibling’ and ‘adopted sibling’ (χ ² = 119,1; df= 3; p= 1,21*10-25; see cd-rom).
Figure 1 : Genetic relatedness and quality of relationship.

In order to visualize the relationship between aspects of social relationships and genetic status, we performed a homogeneity analysis by alternating least squares (HOMALS). This technique, also known as multiple correspondence analysis, allows the descriptive analysis as well as the visual presentation of several variables (see Clausen, 1998). It can be described as a form of principal component analysis for nominal data. No assumptions are made about the distribution of the data. For a further description of the technique we refer to Michailidis and de Leeuw (1998) or the SPSS manual (SPSS, 2001). The common representation of HOMALS is by (just) a two-dimensional graph.[12] Points lying close to each other indicate ‘similarity’, whereas points lying far away from each other indicate categories that discriminate. HOMALS is used here merely for exploring and describing relationships between certain variables, which will then be explored by multinomial logistic regression. More preliminary analyses by HOMALS can be found on the cd-rom.
For the first HOMALS we included interest given to sibling a; interest received from sibling a; genetic status sibling a and quality of relation with sibling a.
Figure 2
: Homogeneity analysis by alternating least squares for genetic status,
interest
received and given and quality of a sibling relationship
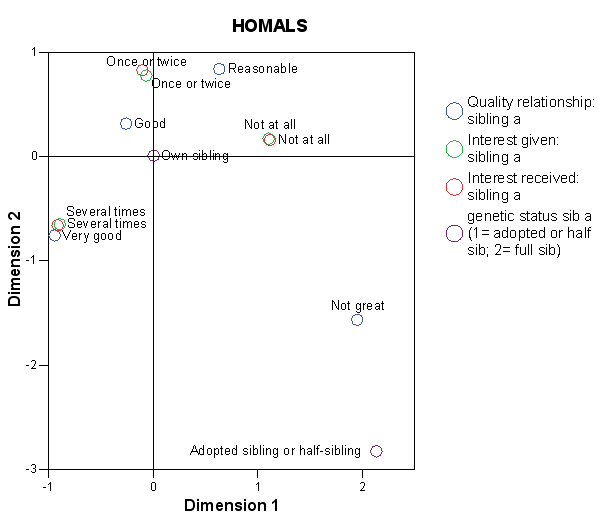
The first dimension distinguishes between a ‘not great’ and a ‘very good relationship’ and between ‘own siblings’ and ‘adopted or half-siblings’.[13] The second dimension distinguishes between ‘good’ and ‘very good’ relationship, and between ‘own siblings’ and ‘adopted or half-siblings’. The HOMALS indicates that ‘interest given and received’ and quality of relationship correspond quite well. Furthermore, respondents appear much more likely to have a good relationship, in which interest is given and received, with their full sibling than with an adopted or half-sibling. On the contrary, if their sibling is a half-sibling or adopted sibling, respondents appear to have a ‘not great’ relationship with their sibling.
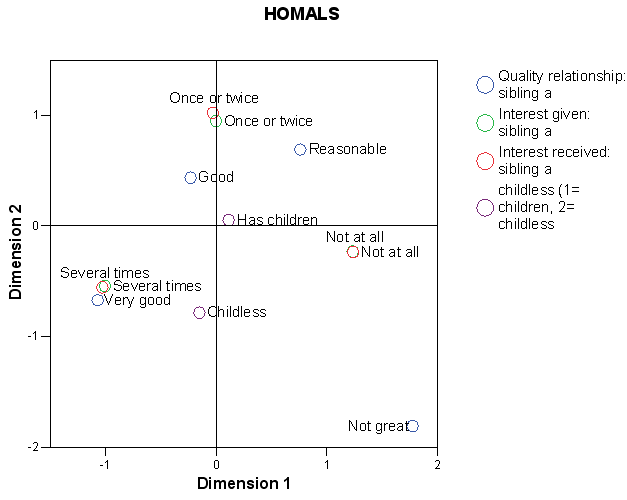
If we replace genetic status of sibling a with childlessness in HOMALS, the following graph shows (Figure 3). The first dimension appears to discriminate between ‘very good’ and ‘not great’ relationships. The second dimension appears to discriminate according to ‘childlessness’ and between ‘good’ and ‘very good relationships’. When examining the second dimension, there is some indication that childless individuals are more likely than ‘parents’ to have a very good instead of a good relationship. The very good relationship is characterized by (strong) ‘mutual interest’.
Figure 3
: Homogeneity analysis by alternating least squares for childlessness,
interest
received and given and quality of a sibling relationship
6.3 Multinomial logistic regression (MLR)
In this section we briefly discuss (multinomial) logistic regression (MLR). Logistic regression is a technique that allows hypothesis testing. The technique is described by Hosmer and Lemeshow (1989), Menard (1995) and Pampel (2000). Logistic regression is relatively free of assumptions and statistically robust. It assumes that there is a linear relation between the independent variable and the logit. If an independent variable has an independent significant effect on the (logit of the) dependent variable, it will be selected in the iterative procedure by which the model is constructed. Whereas estimates in an ordinary least squares (OLS) regression seek to minimize the sum of squared ‘distances’ to the regression line, the parameters in the MLR-model are estimated by maximum likelihood. There are several methods for parameter selection procedure. The method used here is ‘forward stepwise’, yet estimates for correspondent ‘backward stepwise’ models can be found on the cd-rom. In general, the parameter selection procedure did not affect the models presented. In cases where differences between models do occur due to parameter selection procedure, these were only very small differences in terms of model fit and explained variance.
Similar to the equation under multivariate (OLS) regression a multinomial logistic regression equation can be written:
Ln[P(Y=km/kn)/1-P(Y=km/kn)]= a + Σi λi*Xi
With Ln[P(Y=km/kn)/1-P(Y=km/kn)]= the logit for P(Y=km/kn) (the probability that Y is in category m (versus reference category n)); a is the intercept; Xi= independent variable and λi= correspondent parameter for Xi .
Also, similar to OLS regression, a (pseudo-)R² can be calculated. There is a variety of R² measures for logistic regression; we will report Nagelkerke’s (1991) R², as it is most commonly used. For a more in depth discussion of logistic regression we refer to the references cited above.
7. Results from analyses of NKPS
7.1 MLR (main effects) for quality of relationship
The dependent variable for the analysis is ‘quality of relationship with sibling a’.
The (proposed) independent variables and predicted relationships are presented in the table below (Table 3). Most of the predictions can be derived from the theories presented above (2-4). Education is expected to lead to a worse relationship, as higher educated individuals are more ‘individualized’ than lower educated individuals. As the number of (full) living siblings increases the relationship with a random ‘sibling a’ is expected to be worse. Individuals with more siblings have to maintain more relationships. Therefore, it is likely that the quality of a relationship with a randomly assigned sibling is lower.
Although many variables proposed for the model are ‘not biological’, they are necessary for the construction of a model for quality of a relationship with a sibling. Furthermore, we are interested in the effects of ‘biological variables’ while controlling for social variables affecting the quality of a relationship.
Table 3 : Independent variables for the multinomial logistic model
|
Independent variables |
Predicted direction |
|
|
|
|
Sibling a childless
|
Better relationship if sibling a is |
|
|
childless. |
|
Education
|
Worse relation if higher educated. |
|
Age difference between siblings
|
Better relationship if small age |
|
|
difference. |
|
Age |
Better relationship if older. |
|
Sex |
Better relationship if female. |
|
Sex sibling a |
Better relationship if sibling is female. |
|
Childlessness
|
Better relationship if respondent |
|
|
is childless. |
|
Total living (full) siblings |
Worse relationship as number of |
|
|
Increases. |
|
Genetic status |
Better relationship if ‘sibling a’ is a |
|
|
full sibling. |
|
Financial balance |
Better relationship if financially |
|
|
balanced. |
|
Financial help given |
Better if financial help is received |
|
Financial help received |
Better if financial help is given |
|
Interest given |
Better relationship if interest is |
|
|
given. |
|
Interest received |
Better relationship if interest is |
|
|
received. |
|
Initiative contact |
Better relationship if initiative is |
|
|
more or less equal. |
|
Conflict |
Better relationship if there is less |
|
|
conflict. |
As the second dimension in the second HOMALS indicates that the difference between the childless and individuals with children lies between having a good or a very good relationship with sibling a, the reference category for the MLR is set as ‘good’ (Figure 3).
The independent variables presented above were entered in a forward stepwise multinomial logistic regression with as dependent variable quality of relationship. The variables that were selected are presented in the table below (Table 4). The (independent effects of the) variables sex sibling a, sibling a childless, genetic status, age difference did not significantly improve the model (at α= 0,05).
Table 4 : Variables selected for the multinomial logistic model (Step summary)
|
Model |
Effect(s) |
-2 Log Likelihood (-2LL) |
χ² |
df |
p |
|
Step 0 |
Intercept |
10311,05 |
|
|
|
|
Step 1 |
Interest received |
8925,87 |
1385,17 |
6 |
3,92*10-296 |
|
Step 2 |
Financial balance |
8839,76 |
86,11 |
6 |
1,94*10-16 |
|
Step 3 |
Conflict |
8683,33 |
156,43 |
6 |
3,38*10-31 |
|
Step 4 |
Interest given |
8426,74 |
256,59 |
6 |
1,60*10-52 |
|
Step 5 |
Age |
8362,28 |
64,47 |
3 |
6,52*10-14 |
|
Step 6 |
Initiative contact |
8322,80 |
39,47 |
6 |
5,78*10-7 |
|
Step 7 |
Education |
8236,46 |
86,34 |
21 |
6,85*10-10 |
|
Step 8 |
Total living siblings |
8214,18 |
22,28 |
3 |
5,69*10-5 |
|
Step 9 |
Financial help received |
8198,00 |
16,18 |
3 |
0,001 |
|
Step 10 |
Childlessness |
8184,14 |
13,86 |
3 |
0,003 |
|
Step 11 |
Sex |
8174,43 |
9,71 |
3 |
0,021 |
|
Step 12 |
Financial help given |
8165,18 |
9,25 |
3 |
0,026 |
Method: Forward stepwise
The final model has a -2LL of 8165,18 (χ²= 2145,87; df= 69; p<0,001). It has a Nagelkerke R² of 0,43. This is (very) good according to standards in the social sciences. The likelihood ratio tests for the variables are presented in table 5. The χ² tests refer to the difference between -2LL of the final model and the reduced model (Table 5). Reduced model refers to the model without the given variable.
Table 5 : Likelihood ratio tests for the variables in the model
|
Effect |
-2 LL of Reduced Model |
χ² |
df |
p |
|
Intercept |
8165,18 |
0 |
0 |
. |
|
Interest received |
8580,52 |
415,34 |
6 |
1,40*10-86 |
|
Financial balance |
8211,66 |
46,48 |
6 |
2,38*10-8 |
|
Initiative contact |
8993,42 |
828,24 |
6 |
1,22*10-175 |
|
Conflict |
8322,24 |
157,06 |
6 |
2,48*10-31 |
|
Interest given |
8447,46 |
282,28 |
6 |
5,11*10-58 |
|
Education |
8250,79 |
85,61 |
21 |
9,14*10-10 |
|
Sex |
8174,77 |
9,59 |
3 |
0,022 |
|
Age |
9998,35 |
1833,16 |
3 |
<1,22*10-175 |
|
Childlessness |
8178,01 |
12,83 |
3 |
0,005 |
|
Financial help given |
8174,43 |
9,25 |
3 |
0,026 |
|
Financial help received |
8180,33 |
15,15 |
3 |
0,002 |
|
Living siblings |
8185,86 |
20,68 |
3 |
0,0001 |
There appears to be no indication that the parameter selection procedure, forward stepwise, affected the chosen variables.[14] The parameter estimates for each category are presented in separate tables, although they are part of the same analysis. It is important to bear in mind that the comparison of interest is ‘very good’ versus ‘good’ (see: Figure 3). Therefore, we will not (extensively) discuss the other comparisons. The parameter estimates for having a ‘not great’ relationship (versus a good relationship) are presented in table 6. The categories with λ equal to zero are reference categories. Dichotomous variables are treated as interval variables (see: Table 1). The Wald statistic in the tables follows the χ² distribution and allows determining whether or not an individual parameter is statistically significant (Pampel, 2000).
Table 6 : Parameters for ‘not great’ (versus ‘good’) relationship with sibling
|
Quality relationship: |
Not great |
λ |
Std. Error |
Wald |
df |
p |
Exp(λ) |
|
|
Intercept |
0,91 |
2,85 |
0,10 |
1 |
0,748 |
|
|
Interest received |
Not at all |
3,38 |
0,40 |
71,24 |
1 |
3,16*10-17 |
29,31 |
|
|
Once or twice |
1,14 |
0,41 |
7,53 |
1 |
0,006 |
3,12 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Financial balance |
Respondent gives more |
1,26 |
0,68 |
3,41 |
1 |
0,065 |
3,53 |
|
|
More or less equal |
0,38 |
0,67 |
0,32 |
1 |
0,574 |
1,46 |
|
|
Other gives more |
0 |
. |
. |
0 |
. |
. |
|
Initiative contact |
Usually my initiative |
0,35 |
0,35 |
1,03 |
1 |
0,310 |
1,42 |
|
|
More or less equal |
0,22 |
0,33 |
0,42 |
1 |
0,517 |
1,24 |
|
|
Usually other's initiative |
0 |
. |
. |
0 |
. |
. |
|
Conflict |
Not at all |
-4,05 |
0,50 |
65,47 |
1 |
5,90*10-16 |
0,02 |
|
|
Once or twice |
-2,21 |
0,54 |
16,49 |
1 |
4,89*10-5 |
0,11 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Interest given |
Not at all |
2,73 |
0,31 |
75,77 |
1 |
3,19*10-18 |
15,35 |
|
|
Once or twice |
1,07 |
0,32 |
11,60 |
1 |
0,001 |
2,93 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Education |
Incomplete/primary |
-0,84 |
0,32 |
6,65 |
1 |
0,001 |
0,43 |
|
|
Lower vocational |
-1,67 |
0,31 |
28,49 |
1 |
9,403*10-8 |
0,19 |
|
|
Lower general secondary |
-0,92 |
0,32 |
8,46 |
1 |
0,004 |
0,40 |
|
|
Medium general secondary |
-0,74 |
0,44 |
2,91 |
1 |
0,088 |
0,48 |
|
|
Upper general secondary |
0,27 |
0,42 |
0,42 |
1 |
0,518 |
1,31 |
|
|
Intermediate vocational |
-0,79 |
0,29 |
7,23 |
1 |
0,007 |
0,45 |
|
|
Higher vocational |
-0,53 |
0,28 |
3,52 |
1 |
0,061 |
0,59 |
|
|
University or postgraduate |
0 |
. |
|
0 |
. |
. |
|
Sex |
Female |
0,39 |
0,15 |
6,86 |
1 |
0,009 |
1,47 |
|
Age |
Age |
-0,02 |
0,01 |
9,30 |
1 |
0,002 |
0,98 |
|
Childlessness |
Childless |
0,08 |
0,19 |
0,18 |
1 |
0,674 |
1,08 |
|
Financial help given |
No |
0,45 |
0,91 |
0,24 |
1 |
0,624 |
1,56 |
|
Financial help received |
No |
-1,22 |
0,98 |
1,54 |
1 |
0,214 |
0,29 |
|
Living siblings |
Living siblings |
-0,11 |
0,03 |
12,04 |
1 |
0,001 |
0,89 |
Parameters are most easily interpreted in term of odds ratios (Exp(λ); eλ) (Pampel, 2000). For example, women are 1,47 times more likely than men to state that their relationship with their sibling is not great instead of good. This while controlling for the other variables in the model. Another example, individuals who did not receive any interest in their personal life at all are 29,31 times more likely than individuals who received interest several times to have a ‘not great’ relationship instead of a good relationship, while controlling for the other variables.
Perhaps the most interesting, yet intuitive, finding is that a lack of interest (given and received) and the presence conflicts are very strong predictors of having a ‘not great relationship’.
The parameters for a reasonable versus a good relationship (Table 7) and for a very good relationship versus a good relationship (Table 8) are presented below.
Table 7 : Parameters for ‘reasonable’ (versus ‘good’) relationship with sibling
|
Quality relationship: |
Reasonable |
λ |
Std. Error |
Wald |
df |
p |
Exp(λ) |
|
|
Intercept |
3,74 |
1,55 |
5,78 |
1 |
0,016 |
|
|
Interest received |
Not at all |
1,42 |
0,15 |
84,24 |
1 |
4,38*10-20 |
4,13 |
|
|
Once or twice |
0,83 |
0,14 |
35,85 |
1 |
2,13*10-9 |
2,29 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Financial balance |
Respondent gives more |
0,81 |
0,34 |
5,65 |
1 |
0,017 |
2,26 |
|
|
More or less equal |
0,05 |
0,33 |
0,03 |
1 |
0,872 |
1,05 |
|
|
Other gives more |
0 |
. |
. |
0 |
. |
. |
|
Initiative contact |
Usually my initiative |
0,02 |
0,21 |
0,01 |
1 |
0,923 |
1,02 |
|
|
More or less equal |
-0,26 |
0,19 |
1,85 |
1 |
0,173 |
0,77 |
|
|
Usually other's initiative |
0 |
. |
. |
0 |
. |
. |
|
Conflict |
Not at all |
-1,97 |
0,46 |
18,56 |
1 |
1,65*10-5 |
0,14 |
|
|
Once or twice |
-0,93 |
0,48 |
3,67 |
1 |
0,055 |
0,40 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Interest given |
Not at all |
1,47 |
0,15 |
91,66 |
1 |
1,03*10-21 |
4,35 |
|
|
Once or twice |
0,80 |
0,13 |
36,02 |
1 |
1,95*10-9 |
2,23 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Education |
Incomplete/primary |
-0,67 |
0,21 |
10,12 |
1 |
0,001 |
0,51 |
|
|
Lower vocational |
-0,87 |
0,19 |
20,78 |
1 |
5,15*10-6 |
0,42 |
|
|
Lower general secondary |
-0,66 |
0,20 |
11,06 |
1 |
0,001 |
0,52 |
|
|
Medium general secondary |
-0,43 |
0,27 |
2,59 |
1 |
0,108 |
0,65 |
|
|
Upper general secondary |
-0,22 |
0,29 |
0,58 |
1 |
0,447 |
0,80 |
|
|
Intermediate vocational |
-0,46 |
0,18 |
6,46 |
1 |
0,011 |
0,63 |
|
|
Higher vocational |
-0,20 |
0,17 |
1,36 |
1 |
0,243 |
0,82 |
|
|
University or postgraduate |
0 |
. |
. |
0 |
. |
. |
|
Sex |
Female |
0,21 |
0,09 |
5,15 |
1 |
0,023 |
1,24 |
|
Age |
Age |
-0,01 |
0,00 |
7,76 |
1 |
0,005 |
0,99 |
|
Childlessness |
Childless |
0,14 |
0,12 |
1,26 |
1 |
0,262 |
1,15 |
|
Financial help given |
No |
0,23 |
0,52 |
0,19 |
1 |
0,659 |
1,26 |
|
Financial help received |
No |
-1,89 |
0,50 |
14,42 |
1 |
1,46*10-4 |
0,15 |
|
Living siblings |
Living siblings |
-0,05 |
0,02 |
5,29 |
1 |
0,021 |
0,96 |
Table 8 : Parameters for ‘very good’ (versus ‘good’) relationship with sibling
|
Quality relationship: |
Very good |
λ |
Std. Error |
Wald |
df |
p |
Exp(λ) |
|
|
Intercept |
1,60 |
1,44 |
1,24 |
1 |
0,265 |
|
|
Interest received |
Not at all |
-1,15 |
0,17 |
46,69 |
1 |
8,33*10-12 |
0,32 |
|
|
Once or twice |
-0,84 |
0,10 |
67,75 |
1 |
1,86*10-16 |
0,43 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Financial balance |
Respondent gives more |
-0,07 |
0,29 |
0,06 |
1 |
0,810 |
0,93 |
|
|
More or less equal |
-0,02 |
0,25 |
4,49*10-3 |
1 |
0,947 |
0,98 |
|
|
Other gives more |
0 |
. |
. |
0 |
. |
. |
|
Initiative contact |
Usually my initiative |
-0,17 |
0,22 |
0,58 |
1 |
0,446 |
0,84 |
|
|
More or less equal |
0,43 |
0,19 |
5,08 |
1 |
0,024 |
1,54 |
|
|
Usually other's initiative |
0 |
. |
. |
0 |
. |
. |
|
Conflict |
Not at all |
0,66 |
0,81 |
0,66 |
1 |
0,417 |
1,94 |
|
|
Once or twice |
0,04 |
0,84 |
0,00 |
1 |
0,962 |
1,04 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Interest given |
Not at all |
-0,87 |
0,16 |
29,21 |
1 |
6,50*10-8 |
0,42 |
|
|
Once or twice |
-0,62 |
0,10 |
37,79 |
1 |
7,89*10-10 |
0,54 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Education |
Incomplete/primary |
0,03 |
0,19 |
0,03 |
1 |
0,865 |
1,03 |
|
|
Lower vocational |
0,06 |
0,17 |
0,12 |
1 |
0,733 |
1,06 |
|
|
Lower general secondary |
0,17 |
0,18 |
0,96 |
1 |
0,327 |
1,19 |
|
|
Medium general secondary |
-0,30 |
0,26 |
1,38 |
1 |
0,241 |
0,74 |
|
|
Upper general secondary |
-0,21 |
0,27 |
0,57 |
1 |
0,450 |
0,81 |
|
|
Intermediate vocational |
-0,23 |
0,17 |
1,82 |
1 |
0,177 |
0,79 |
|
|
Higher vocational |
-0,24 |
0,16 |
2,21 |
1 |
0,137 |
0,79 |
|
|
University or postgraduate |
0 |
. |
. |
0 |
. |
. |
|
Sex |
Female |
0,09 |
0,09 |
1,13 |
1 |
0,287 |
1,10 |
|
Age |
Age |
0,02 |
0,00 |
25,37 |
1 |
4,74*10-7 |
1,02 |
|
Childlessness |
Childless |
0,39 |
0,11 |
12,78 |
1 |
3,50*10-4 |
1,47 |
|
Financial help given |
No |
-0,91 |
0,33 |
7,74 |
1 |
0,005 |
0,40 |
|
Financial help received |
No |
-0,90 |
0,47 |
3,57 |
1 |
0,059 |
0,41 |
|
Living siblings |
Living siblings |
-0,06 |
0,02 |
8,59 |
1 |
0,003 |
0,95 |
7.2 Discussion of MLR for relationship quality
7.2.1 Variable selection
As expected most variables were selected as predictors for ‘quality of relationship with sibling a’. Social factors, e.g. interest, were highly significant predictors of relationship quality. However, genetic status, age difference, sibling a childless and sex sibling a were not found to be significant (independent) predictors of relationship quality.
Especially, for genetic status, this is puzzling. A possible explanation for the non-selection of genetic status as predictor is that other variables in the model are far stronger predictors of quality of the relationship. For instance, ‘interest received’ and ‘interest given’ are very strong predictors. However, if genetic status is a significant predictor of ‘interest’ variables, it is possible that it influences the quality of a relationship in an indirect way.[15] As can be seen in the figure below, genetic status does significantly relate to ‘interest received’ (χ²= 13,81; df= 2; p= 0,001) but not to ‘interest given’ (χ²= 5,60; df= 2; p= 0,061).[16] Respondents are significantly more likely to receive interest from a full sibling than from an adopted or half-sibling.[17] Under 7.4.1 and 7.4.2, we will further analyze the effect of genetic relatedness on interest given and interest received.
Genetic status also varies according to attained level of education (χ²= 24,14; df= 7; p=0,001; Table 9). In addition, ‘genetic status of sibling a’ obviously relates to ‘total full living siblings’ (r= 0,183; p= 1,02*10-36; n = 4710). Effects of genetic status on these variables could explain why it is not selected as predictor for quality of relationship with sibling a. Similar analyses for genetic status and other parameters in our model, such as ‘initiative of contact’ of ‘giving financial help’, were not significant and can be found on the cd-rom (α = 0,05).
Figure 4 : Genetic relatedness and interest [18]
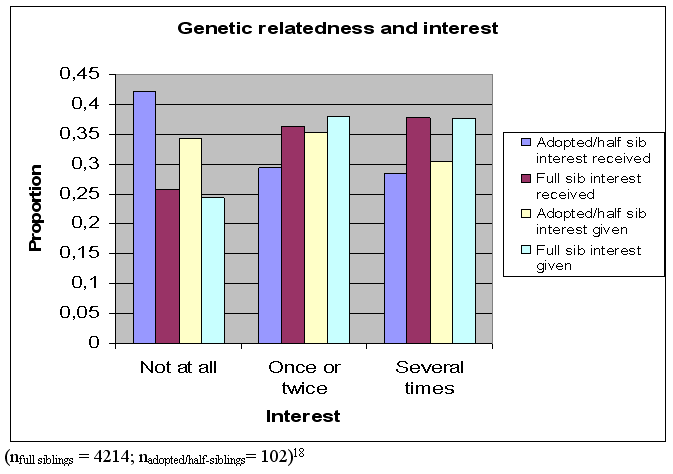
Table 9 : Frequency table for education by genetic status
|
|
Incomplete/ primary |
Lower voc. |
Lower gen. Sec. |
Medium gen. sec. |
Upper gen. sec. |
Inter. voc. |
higher voc. |
University |
Total |
|
Adopted/half-sibling |
28 |
29 |
25 |
11 |
12 |
26 |
25 |
8 |
164 |
|
Own sibling |
517 |
806 |
617 |
171 |
146 |
811 |
1078 |
395 |
4541 |
|
Total |
545 |
835 |
642 |
182 |
158 |
837 |
1103 |
403 |
4705 |
Omitting ‘interest received’, ‘total living own siblings’ and ‘education’, leads to a model with a Nagelkerke R² of 0,35 (final model: -2LL= 8169,62; χ²= 1644,82; df= 39; p<0,001). This is still (very) good according to standards in the social sciences. It is important to note that we assigned ‘not great’ as the reference category (see: Figure 1). In this model, genetic status is a significant predictor at five percent significance level (Table 10).[19] Here we present only the parameters for the comparison between ‘not great’ and ‘good’ and between ‘not great’ and ‘very good’. The parameter estimates for ‘not great’ versus ‘reasonable’ can be found on the cd-rom.
Table 10 : Step summary for model with genetic status
|
Model |
Effect(s) |
-2LL |
χ² |
df |
p |
|
Step 0 |
Intercept |
9814,44 |
|
|
|
|
Step 1 |
Interest given |
8749,22 |
1065,22 |
6 |
6,99*10-227 |
|
Step 2 |
Conflict |
8499,12 |
250,11 |
6 |
3,89*10-51 |
|
Step 3 |
Initiative contact |
8357,88 |
141,23 |
6 |
5,5*10-28 |
|
Step 4 |
Financial balance |
8289,91 |
67,97 |
6 |
1,07*10-12 |
|
Step 5 |
Age |
8223,86 |
66,05 |
3 |
2,99*10-14 |
|
Step 6 |
Childlessness |
8205,38 |
18,48 |
3 |
3,5*10-4 |
|
Step 7 |
Financial help received |
8190,06 |
15,32 |
3 |
0,002 |
|
Step 8 |
Financial help given |
8177,85 |
12,21 |
3 |
0,007 |
|
Step 9 |
Genetic status sibling |
8169,62 |
8,23 |
3 |
0,041 |
Method: Forward stepwise
Table 11 : Likelihood ratio tests for model with genetic interest
|
Effect |
-2LL |
χ² |
df |
p |
|
Intercept |
8169,62 |
0 |
0 |
. |
|
Interest given |
9263,09 |
1093,48 |
6 |
5,38*10-233 |
|
Conflict |
8345,01 |
175,4 |
6 |
3,22*10-35 |
|
Initiative contact |
8237,13 |
67,51 |
6 |
1,32*10-12 |
|
Financial balance |
8245,07 |
75,46 |
6 |
3,09*10-14 |
|
Age |
8237,59 |
67,97 |
3 |
1,16*10-14 |
|
Genetic status sibling |
8177,85 |
8,23 |
3 |
0,041 |
|
Financial help given |
8181,9 |
12,28 |
3 |
0,006 |
|
Financial help received |
8184,29 |
14,67 |
3 |
0,002 |
|
Childlessness |
8185,71 |
16,1 |
3 |
0,001 |
If the respondent’s sibling is a full sibling, he or she is approximately two and half times more likely to have a good, instead of a ‘not great’ relationship with them, than when the sibling is an adopted or half-sibling (Table 12). When comparing a very good versus a not great relationship, full siblings are 2,75 more likely than not fully related siblings to have a very good relationship versus a not great relationship (Table 13). Both effects of genetic relatedness are found while controlling for other variables in the model.[20] However, if we control for ‘interest received’, we find no significant (independent) effect of genetic relatedness on relationship quality (see cd-rom).
Table 12 : Parameter estimates for ‘good’ versus ‘not great’ relationship
|
Quality relationship: |
Good |
λ |
Std. Error |
Wald |
df |
p |
Exp(λ) |
|
|
Intercept |
-2,92 |
2,67 |
1,2 |
1 |
0,274 |
|
|
Interest given |
Not at all |
-3,96 |
0,28 |
205,88 |
1 |
1,09*10-46 |
0,02 |
|
|
Once or twice |
-1,53 |
0,29 |
28,58 |
1 |
9*10-8 |
0,22 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Conflict |
Not at all |
3,99 |
0,47 |
71,06 |
1 |
3,47*10-17 |
53,86 |
|
|
Once or twice |
2,21 |
0,51 |
18,75 |
1 |
1,49*10-5 |
9,15 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Initiative contact |
Usually my initiative |
-0,55 |
0,33 |
2,74 |
1 |
0,098 |
0,58 |
|
|
More or less equal |
-0,14 |
0,32 |
0,2 |
1 |
0,653 |
0,87 |
|
|
Usually other's initiative |
0 |
. |
. |
0 |
. |
. |
|
Financial balance |
Respondent gives more |
-1,83 |
0,67 |
7,53 |
1 |
0,006 |
0,16 |
|
|
More or less equal |
-0,78 |
0,65 |
1,41 |
1 |
0,234 |
0,46 |
|
|
Other gives more |
0 |
. |
. |
0 |
. |
. |
|
Age |
Age |
0,02 |
0,01 |
12,03 |
1 |
0,001 |
1,02 |
|
Genetic relatedness |
Full sibling |
0,92 |
0,34 |
7,34 |
1 |
0,007 |
2,51 |
|
Financial help given |
No |
-0,48 |
0,88 |
0,29 |
1 |
0,588 |
0,62 |
|
Financial help received |
No |
1,44 |
0,85 |
2,88 |
1 |
0,09 |
4,24 |
|
Childlessness |
Childless |
-0,28 |
0,18 |
2,41 |
1 |
0,12 |
0,76 |
Table 13 : Parameter estimates for ‘very good’ versus ‘not great’ relationship
|
Quality relationship: |
Very good |
λ |
Std. Error |
Wald |
df |
p |
Exp(λ) |
|
|
Intercept |
-1,86 |
2,81 |
0,44 |
1 |
0,508 |
|
|
Interest given |
Not at all |
-5,46 |
0,3 |
334,15 |
1 |
1,19*10-74 |
0,004 |
|
|
Once or twice |
-2,58 |
0,29 |
77,79 |
1 |
1,15*10-18 |
0,08 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Conflict |
Not at all |
4,86 |
0,81 |
36,21 |
1 |
1,77*10-9 |
128,8 |
|
|
Once or twice |
2,54 |
0,85 |
8,96 |
1 |
0,003 |
12,64 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Initiative contact |
Usually my initiative |
-0,9 |
0,38 |
5,77 |
1 |
0,016 |
0,41 |
|
|
More or less equal |
0,23 |
0,35 |
0,41 |
1 |
0,522 |
1,25 |
|
|
Usually other's initiative |
0 |
. |
. |
0 |
. |
. |
|
Financial balance |
Respondent gives more |
-2,18 |
0,7 |
9,69 |
1 |
0,002 |
0,11 |
|
|
More or less equal |
-0,95 |
0,68 |
1,95 |
1 |
0,163 |
0,39 |
|
|
Other gives more |
0 |
. |
. |
0 |
. |
. |
|
Age |
Age |
0,04 |
0,01 |
38,36 |
1 |
5,89*10-10 |
1,05 |
|
Genetic relatedness |
Full sibling |
1,01 |
0,42 |
5,84 |
1 |
0,016 |
2,75 |
|
Financial help given |
No |
-1,5 |
0,9 |
2,81 |
1 |
0,094 |
0,22 |
|
Financial help received |
No |
0,42 |
0,85 |
0,24 |
1 |
0,625 |
1,52 |
|
Childlessness |
Childless |
0,12 |
0,2 |
0,37 |
1 |
0,542 |
1,13 |
The direct and indirect effects of genetic status on relationship quality could be further explored by logistic path models (Eshima et al., 2001) or structural equation modelling (Loehlin, 2004; see cd-rom for example).
Similar to genetic status, childlessness of the sibling does not (independently) appear to affect the quality of the relationship (in our initial model). However, we should take into account that the question about relationship quality was asked to the anchor and not to the sibling.[21] Sex of the sibling did not (independently) affect the quality of the relationship, contrary to the expectation that women would have better relationships with our kin. Yet, this could be due to the fact that the question was asked to the anchor and not to the sibling. Age difference between the siblings did not (independently) affect the quality of the relationship. This could be due to the selection of respondents aged over forty; (relative) age difference might not be that relevant as individuals grow older. Moreover, we should bear in mind that age difference, the difference between birth years, is not a completely accurate representation of age difference between the siblings.
7.2.2 Comparison good versus very good relationship
In general, the direction of the variables that were selected for the initial model was in the expected direction (Table 14). Although, some parameter estimates were not significant in the comparison of a good versus very good relationship, the direction of the parameter estimates in the comparisons of ‘not great’ or ‘reasonable’ versus ‘good’ was generally consistent with the predicted relationships for most variables. A model with reference category set as ‘not great’, which can be found on the cd-rom, more clearly shows that (nearly all) the parameter estimates are in the predicted direction.
‘Giving financial help’ and ‘giving and receiving interest’ are (highly) significant predictors of having a very good relationship (Table 8). This supports the idea that high quality relationships go together with (mutual) investments in terms of time and money. As predicted childless individuals were also significantly, nearly one and a half time, more likely than parents to have a very good relationship, instead of a good relationship, while controlling for other variables (Table 8).
Table 14 : Results compared with predictions for comparison of ‘good’ versus ‘very good’ relationship.
|
Independent variables |
Predicted direction |
Model (good vs. |
|
|
|
very good) |
|
Sibling a childless |
Better relationship if sibling a is |
Not significant |
|
|
childless. |
|
|
Education |
Better relation if higher educated. |
Not significant |
|
|
|
(mixed direction) |
|
Age difference |
Better relationship if small age |
Not significant |
|
|
Difference. |
|
|
Age |
Better relationship if older. |
As predicted |
|
Sex |
Better relationship if female. |
Not significant |
|
|
|
(correct direction) |
|
Sex sibling a |
Better relationship if sibling is female. |
Not significant |
|
Childlessness |
Better relationship if respondent |
As predicted |
|
|
is childless. |
|
|
Total living (full) |
Worse relationship as number of |
As predicted |
|
siblings |
increases. |
|
|
Genetic status |
Better relationship if sibling a is a |
Not significant |
|
|
full sibling. |
|
|
Financial balance |
Better relationship if financially |
Not significant |
|
|
balanced. |
(mixed direction) |
|
Financial help given |
Better if financial help is received |
As predicted |
|
Financial help received |
Better if financial help is given |
Not significant |
|
|
|
(correct direction) |
|
Interest given |
Better relationship if interest is |
As predicted |
|
|
given. |
|
|
Interest received |
Better relationship if interest is |
As predicted |
|
|
received. |
|
|
Initiative contact |
Better relationship if initiative is |
As predicted |
|
|
more or less equal. |
|
|
Conflict |
Better relationship if there is less |
Not significant |
|
|
conflict. |
(correct direction) |
7.3 MLR with interaction effects for relationship quality
Although, the base model with just the main effects is perfectly valid (see, Peng et al., 2002), the model could be further improved by incorporating interaction effects. We explored all two-way interaction effects.[22] Only the interaction effects between sex of the respondent and financial help received and between age and financial help received were found significant predictors of relationship quality (α = 0,05). The model including interaction terms is only marginally better than the previous model (Nagelkerke R²= 0,44; -2LL= 8144,48; χ²= 2166,57; df=78; p<0,001). The statistics and parameters estimates for this model can therefore be found on the cd-rom.
Interestingly, none of the interaction effects between childlessness and other independent variables were found significant (α = 0,05). There were also no significant interaction effects between genetic relatedness and other variables (α = 0,05).[23] Also of interest is that there is no interaction effect for interest given and interest received or for financial help given and received.
Moreover, there was no significant interaction effect for ‘childlessness’ and ‘sibling a childless’. We would expect that the relationship would be better if the anchor is childless but the sibling has children. It is possible that childless individuals are closer to their sibling regardless of whether they have children are not. Also, the absence of an interaction effect could be due to the fact that the respondents are over forty years, therefore their nieces and nephews are probably self-sufficient. Although, an analysis for childless individuals appears to indicate that the relationship is in fact better if the sibling has children (Somers’ Dyx = -0,071; one-tailed p= 0,051; n= 818; Figure 5).
Figure 5 : Sibling childlessness and quality of relationship for childless respondents
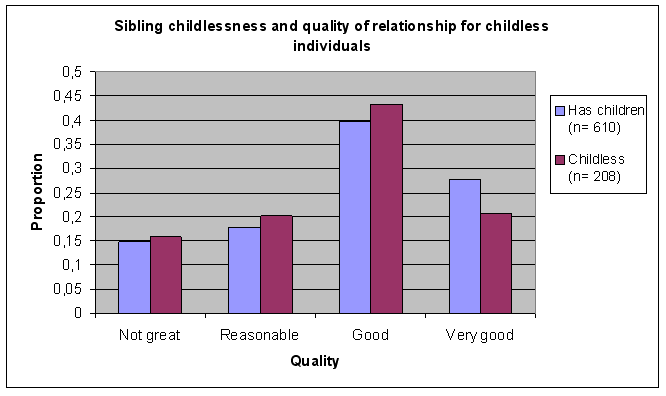
7.4 MLR for ‘investment measures’ of relationships
Although we have shown that childless individuals have ‘better’ relationships with their siblings than parents, and that these ‘better’ relationships go together with some ‘investments’ (giving interest and giving financial help), we have not yet shown that childless individuals actually ‘invest’ in these relationships.
For this section, we are mainly interested in how childlessness and genetic relatedness influences ‘investment measures’ while controlling for other relation aspects. Therefore we will not report and discuss all models in detail. All the models and their statistics can be found in full on the cd-rom. ‘Forward stepwise’ was used as method for parameter selection. The parameter selection procedure generally did not affect the selected variables. However in some cases, the backwards stepwise procedure leads to (marginally) different results, which can be found on the cd-rom. As predictor variables we select the other previously used variables, excluding ‘quality of relationship’ (Table 1). These variables are included in our models, as we want to investigate the (independent) effects of childlessness and genetic relatedness, while controlling for other (social) factors influencing the sibling relationship. For these models, we will only investigate the main effects.
By ‘investment’ measures, we refer to ‘giving interest’, ‘giving financial help’, ‘financial balance’ (giving more than receiving) and ‘initiative of contact’ (showing initiative). Although the cost of such investments is not always large, these variables do represent a cost in time or money and an opportunity cost, i.e. investment in other relationships. Childless individuals are predicted to ‘invest’ more than ‘parents’. If siblings are closer related they are also predicted to invest more.
7.4.1 Giving interest
The model shows no significant (independent) effect for childlessness and genetic status (Table 15). There were also no significant (independent) effects for sibling a childless, sex sibling a, age difference, age, financial help given/received and initiative of contact. The model has a Nagelkerke R² of 0,48 (-2LL= 6892,94; χ²= 2400,55; df=30; p<0,001). The parameter estimates as well as the step summary for this model can be found on the cd-rom.
Table 15 : Likelihood ratio tests for model for ‘interest given’
|
Effect |
-2 LL |
χ² |
df |
p |
|
Intercept |
6615,83 |
0,00 |
0 |
. |
|
Financial balance |
6645,29 |
29,46 |
4 |
6,30*10-6 |
|
Conflict |
6631,05 |
15,22 |
4 |
0,004 |
|
Interest received |
8692,19 |
2076,36 |
4 |
<9,9*10-19 |
|
Education |
6662,89 |
47,06 |
14 |
1,88*10-5 |
|
Sex |
6698,74 |
82,91 |
2 |
9,9*10-19 |
|
Living siblings |
6626,43 |
10,60 |
2 |
0,005 |
However, if we omit ‘interest received’, which is a very strong predictor[24] of ‘interest given’, from the model we do find effects for childlessness and genetic relatedness (Table 16). This alternative model has a Nagelkerke R² of 0,11, which is reasonable for the social sciences (-2LL= 8850,78; χ²= 442,71; df=38; p<0,001). Age, financial balance and childlessness of sibling a were not significant (independent) predictors of ‘giving interest’.
Table 16 : Likelihood ratio tests for model for ‘interest given’ (omission of interest received)
|
Effect |
-2 LL |
χ² |
df |
p |
|
Intercept |
8573,66 |
0,00 |
0 |
. |
|
Initiative contact |
8605,88 |
32,22 |
4 |
1,73*10-6 |
|
Conflict |
8598,89 |
25,23 |
4 |
4,53*10-5 |
|
Education |
8659,36 |
85,69 |
14 |
2,45*10-12 |
|
Sex |
8741,92 |
168,26 |
2 |
2,91*10-37 |
|
Genetic status sibling |
8580,46 |
6,79 |
2 |
0,033 |
|
Age difference |
8581,61 |
7,95 |
2 |
0,019 |
|
Sex sibling |
8621,36 |
47,70 |
2 |
4,38*10-11 |
|
Childlessness |
8582,90 |
9,24 |
2 |
0,01 |
|
Living siblings |
8608,66 |
35,00 |
2 |
2,51*10-8 |
|
Financial help given |
8585,38 |
11,71 |
2 |
0,003 |
|
Financial help received |
8580,33 |
6,66 |
2 |
0,036 |
Childless individuals are 1,36 times more likely than ‘parents’ to have given interest to their sibling several times over the past three months, instead of not at all (Table 17). This while controlling for the other variables in the model. Respondents are 2,04 times more likely to have given interest several times, instead of not at all, to a full sibling than to an adopted or half-sibling and this while controlling for the other variables in the model. The parameter estimates for the comparison between interest given ‘once or twice’ versus ‘not at all’ can be found on the cd-rom.
Table 17 : Parameter estimates for ‘interest given several times’ (versus not at all)
|
Interest given: |
Several times |
λ |
Std. Error |
Wald |
df |
p |
Exp(λ) |
|
|
Intercept |
3,05 |
1,87 |
2,68 |
1 |
0,102 |
|
|
Initiative contact |
Usually my initiative |
-0,34 |
0,20 |
2,83 |
1 |
0,092 |
0,71 |
|
|
More or less equal |
0,20 |
0,19 |
1,14 |
1 |
0,286 |
1,22 |
|
|
Usually other's initiative |
0,00 |
. |
. |
0 |
. |
. |
|
Conflict |
Not at all |
0,98 |
0,30 |
10,37 |
1 |
0,001 |
2,67 |
|
|
Once or twice |
1,36 |
0,36 |
14,18 |
1 |
1,66*10-4 |
3,90 |
|
|
Several times |
0,00 |
. |
. |
0 |
. |
. |
|
Education |
Incomplete/primary |
-1,16 |
0,20 |
34,52 |
1 |
4,22*10-9 |
0,31 |
|
|
Lower vocational |
-0,96 |
0,18 |
27,00 |
1 |
2,04*10-7 |
0,38 |
|
|
Lower general secondary |
-0,80 |
0,19 |
16,93 |
1 |
3,89*10-5 |
0,45 |
|
|
Medium general secondary |
-0,55 |
0,26 |
4,26 |
1 |
0,039 |
0,58 |
|
|
Upper general secondary |
-0,32 |
0,29 |
1,27 |
1 |
0,260 |
0,72 |
|
|
Intermediate vocational |
-0,69 |
0,18 |
14,34 |
1 |
1,53*10-4 |
0,50 |
|
|
Higher vocational |
-0,24 |
0,18 |
1,79 |
1 |
0,181 |
0,79 |
|
|
University or postgraduate |
0,00 |
. |
. |
0 |
. |
. |
|
Sex |
Female |
1,08 |
0,09 |
153,40 |
1 |
3,13*10-35 |
2,94 |
|
Genetic status sibling |
Full sibling |
0,71 |
0,27 |
6,74 |
1 |
0,009 |
2,04 |
|
Age difference |
Age difference |
-0,03 |
0,01 |
7,65 |
1 |
0,006 |
0,97 |
|
Sex sibling |
Female |
0,57 |
0,08 |
46,23 |
1 |
1,05*10-11 |
1,77 |
|
Living siblings |
Living siblings |
-0,11 |
0,02 |
30,98 |
1 |
2,61*10-8 |
0,90 |
|
Financial help given |
No |
-1,00 |
0,44 |
5,23 |
1 |
0,022 |
0,37 |
|
Financial help received |
No |
-1,61 |
0,76 |
4,52 |
1 |
0,033 |
0,20 |
|
Childlessness |
Childless |
0,31 |
0,11 |
7,20 |
1 |
0,007 |
1,36 |
|
|
|
|
|
|
|
|
|
Yet, if we control for interest received, we find no significant (independent) effects for childlessness and genetic relatedness.
7.4.2 Receiving interest
The model has a Nagelkerke R² of 0,51 (-2LL= 6787,49; χ²= 2557,36; df=28; p<0,001). Childlessness, education, age, sex and financial help received were not significant predictors of receiving interest (Table 18). Childlessness does not appear to independently affect the personal interest received from a sibling.
Table 18 : Likelihood ratio tests for model for ‘interest received’
|
Effect |
-2 LL |
χ² |
df |
p |
|
Intercept |
6787,49 |
0,00 |
0 |
. |
|
Financial balance |
6854,25 |
66,76 |
4 |
1,10*10-13 |
|
Initiative contact |
6862,71 |
75,22 |
4 |
1,79*10-15 |
|
Conflict |
6802,96 |
15,47 |
4 |
0,004 |
|
Genetic status sibling |
6794,84 |
7,35 |
2 |
0,025 |
|
Age difference |
6793,57 |
6,07 |
2 |
0,048 |
|
Sex sibling |
6822,59 |
35,10 |
2 |
2,39*10-8 |
|
Childlessness of sibling |
6796,72 |
9,23 |
2 |
0,01 |
|
Living siblings |
6800,06 |
12,57 |
2 |
0,002 |
|
Financial help given |
6793,83 |
6,34 |
2 |
0,042 |
|
Interest given |
8903,19 |
2115,70 |
4 |
<1,79*10-15 |
Individuals are 1,93 times more likely to have received interest once or twice, instead of not at all, during the past three months if their sibling is a full sibling instead of an adopted or half-sibling (Table 19). This while controlling for the other variables. Respondents are 1,45 times more likely to have received interest once or twice over the past three months instead of not at all from a sibling who has children, than from a childless sibling.[25] This is contrary to our predictions, as we would expect that they would have received more interest in their personal life if their sibling was childless.
Table 19 : Parameter estimates for ‘interest received once or twice’ (versus not at all)
|
Interest received: |
Once or twice |
λ |
Std. Error |
Wald |
df |
p |
Exp(λ) |
|
|
Intercept |
-2,45 |
1,45 |
2,86 |
1 |
0,091 |
|
|
Financial balance |
Respondent gives more |
-0,67 |
0,41 |
2,74 |
1 |
0,098 |
0,51 |
|
|
More or less equal |
-0,13 |
0,39 |
0,11 |
1 |
0,739 |
0,88 |
|
|
Other gives more |
0,00 |
. |
. |
0 |
. |
. |
|
Initiative contact |
Usually my initiative |
-0,25 |
0,23 |
1,20 |
1 |
0,274 |
0,78 |
|
|
More or less equal |
0,30 |
0,21 |
1,92 |
1 |
0,165 |
1,35 |
|
|
Usually other's initiative |
0,00 |
. |
. |
0 |
. |
. |
|
Conflict |
Not at all |
0,92 |
0,34 |
7,13 |
1 |
0,008 |
2,50 |
|
|
Once or twice |
0,70 |
0,39 |
3,23 |
1 |
0,072 |
2,01 |
|
|
Several times |
0,00 |
. |
. |
0 |
. |
. |
|
Genetic status sibling |
Full sibling |
0,66 |
0,29 |
5,26 |
1 |
0,022 |
1,93 |
|
Age difference |
Age difference |
-0,03 |
0,01 |
6,05 |
1 |
0,014 |
0,97 |
|
Sex sibling |
Female |
0,43 |
0,09 |
22,06 |
1 |
2,64*10-6 |
1,54 |
|
Sibling childlessness |
Childless |
-0,37 |
0,12 |
9,18 |
1 |
0,002 |
0,69 |
|
Living siblings |
Living siblings |
-0,05 |
0,02 |
7,32 |
1 |
0,007 |
0,95 |
|
Financial help given |
No |
0,98 |
0,61 |
2,57 |
1 |
0,109 |
2,67 |
|
Interest given |
Not at all |
-2,52 |
0,14 |
304,12 |
1 |
4,16*10-68 |
0,08 |
|
|
Once or twice |
-0,19 |
0,14 |
2,00 |
1 |
0,157 |
0,82 |
|
|
Several times |
0,00 |
. |
. |
0 |
. |
. |
Individuals are 2,32 times more likely to have received interest several times, instead of not at all, during the past three months from a full sibling than from an adopted or half-sibling (Table 20). This while controlling for other variables in the model. The parameter estimate for sibling childlessness is not significant for the comparison between interest received ‘several times’ versus ‘not at all’.
Table 20 : Parameter estimates for ‘interest received several times’ (versus not at all)
|
Interest received: |
Several times |
λ |
Std. Error |
Wald |
df |
p |
Exp(λ) |
|
|
Intercept |
1,29 |
1,43 |
0,81 |
1 |
0,369 |
|
|
Financial balance |
Respondent gives more |
-2,12 |
0,41 |
26,53 |
1 |
2,59*10-7 |
0,12 |
|
|
More or less equal |
-0,98 |
0,39 |
6,38 |
1 |
0,012 |
0,37 |
|
|
Other gives more |
0,00 |
. |
. |
0 |
. |
. |
|
Initiative contact |
Usually my initiative |
-1,14 |
0,25 |
20,61 |
1 |
5,63*10-6 |
0,32 |
|
|
More or less equal |
0,02 |
0,23 |
0,01 |
1 |
0,918 |
1,02 |
|
|
Usually other's initiative |
0,00 |
. |
. |
0 |
. |
. |
|
Conflict |
Not at all |
1,62 |
0,47 |
11,81 |
1 |
0,001 |
5,07 |
|
|
Once or twice |
1,34 |
0,51 |
6,77 |
1 |
0,009 |
3,81 |
|
|
Several times |
0,00 |
. |
. |
0 |
. |
. |
|
Genetic status sibling |
Full sibling |
0,84 |
0,34 |
6,13 |
1 |
0,013 |
2,32 |
|
Age difference |
Age difference |
-0,02 |
0,01 |
1,95 |
1 |
0,163 |
0,98 |
|
Sex sibling |
Female |
0,60 |
0,10 |
33,19 |
1 |
8,38*10-9 |
1,83 |
|
Sibling childlessness |
Childless |
-0,23 |
0,14 |
2,90 |
1 |
0,089 |
0,79 |
|
Living siblings |
Living siblings |
-0,08 |
0,02 |
12,00 |
1 |
0,001 |
0,92 |
|
Financial help given |
No |
-0,19 |
0,56 |
0,12 |
1 |
0,733 |
0,83 |
|
Interest given |
Not at all |
-4,86 |
0,17 |
849,44 |
1 |
9,64*10-187 |
0,01 |
|
|
Once or twice |
-2,49 |
0,14 |
313,08 |
1 |
4,66*10-70 |
0,08 |
|
|
Several times |
0,00 |
. |
. |
0 |
. |
. |
If ‘interest given’ is omitted from the model, ‘childlessness’ is a significant predictor for interest received. Yet, the parameter estimates for childlessness are not significant. This model can be found on the cd-rom.
7.4.3 Giving and receiving interest
Through a combination of both measures above, we can analyze imbalances in interest given and interest received in each other’s personal life. The differences in interest given and received between dyads of full siblings and dyads where the siblings are not fully related are significant (χ²= 15,87; df=8; p= 0,044; Figure 6).[26] Approximately one quarter of the sibling dyads where the siblings are not fully related, can be characterized by ‘no interest given and no interest received’. For relationships where the sibling is adopted or a half-sibling, in approximately forty percent of the cases the respondent received no interest in the past three months (see: Figure 4).
Figure 6 : Genetic relatedness and interest given and received
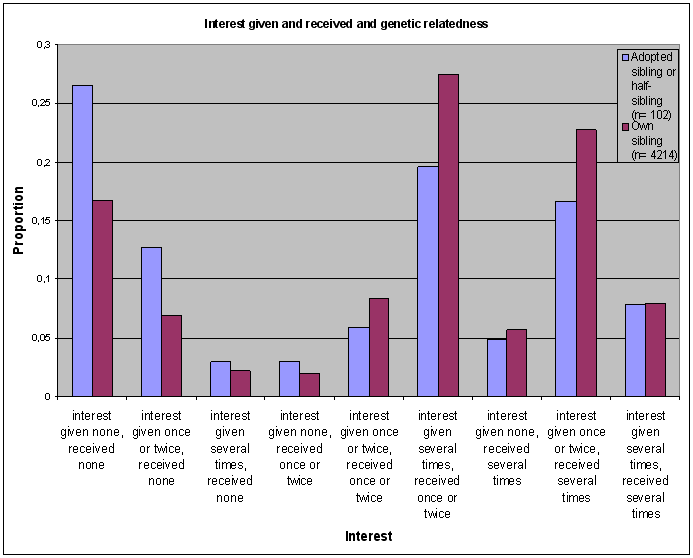
Childless individuals are (significantly) more likely than ‘parents’ to have given interest several times but have only received interest once or twice’ over the past three months (Figure 7). For childless individuals, over one third of the dyads can be characterized as ‘interest given several times but only received once or twice’ over the past three months. The differences between childless individuals and ‘parents’ are significant (χ²= 28,04; df= 8; p= 4,66*10-4).[27]
Figure 7 : Childlessness and interest given and received
A multinomial logistic regression model for ‘interest given and received’, with reference category ‘interest given none, received none’ was constructed. This allows investigating the effect of genetic relatedness. The model has a Nagelkerke R² of 0,20 (-2LL= 15453,16; χ²= 949,14; df= 176; p<0,001; Table 21). Sibling childlessness did not independently influence ‘interest given and received’.
Table 21 : Likelihood ratio tests for interest given and received
|
Effect |
-2 LL |
χ² |
df |
p |
|
Intercept |
15453,17 |
0 |
0 |
. |
|
Genetic status sibling |
15468,79 |
15,62 |
8 |
0,048 |
|
Age difference |
15469,23 |
16,06 |
8 |
0,042 |
|
Sex sibling |
15533,06 |
79,90 |
8 |
5,13*10-14 |
|
Childlessness |
15473,59 |
20,42 |
8 |
0,009 |
|
Education |
15593,82 |
140,66 |
56 |
3,14*10-9 |
|
Financial balance |
15537,27 |
84,10 |
16 |
3,01*10-11 |
|
Initiative contact |
15571 |
117,84 |
16 |
1,43*10-17 |
|
Conflict |
15501,14 |
47,98 |
16 |
4,79*10-5 |
|
Sex |
15634,03 |
180,87 |
8 |
6,78*10-35 |
|
Age |
15473,53 |
20,36 |
8 |
0,009 |
|
Living siblings |
15501,96 |
48,79 |
8 |
6,97*10-8 |
|
Financial help received |
15473,76 |
20,59 |
8 |
0,008 |
|
Financial help given |
15471,06 |
17,90 |
8 |
0,022 |
Full siblings are 2,25 times more likely than not fully
related siblings to have a relationship in which interest was given
and received once or twice over the past
three months, instead of ‘no interest given and
received at all’ (Table 22). This while controlling for other variables in the model.
The other parameter estimates for this model can be found on the cd-rom.
Table 22 : Parameter estimates for interest given and received once or twice (versus interest given and received: not at all)
|
Interest given and received |
Once or twice |
λ |
Std. Error |
Wald |
df |
p |
Exp(λ) |
|
|
Intercept |
0,18 |
2,78 |
0,00 |
1 |
0,949 |
|
|
Genetic status sibling |
Full sibling |
0,81 |
0,33 |
6,03 |
1 |
0,014 |
2,25 |
|
Age difference |
Age difference |
-0,02 |
0,01 |
3,58 |
1 |
0,058 |
0,98 |
|
Sex sibling |
Female |
0,50 |
0,10 |
24,00 |
1 |
9,62*10-7 |
1,65 |
|
Childless |
Childless |
-0,11 |
0,14 |
0,63 |
1 |
0,428 |
0,90 |
|
Education |
Incomplete/primary |
-1,27 |
0,24 |
27,06 |
1 |
1,98*10-7 |
0,28 |
|
|
Lower vocational |
-1,14 |
0,22 |
25,70 |
1 |
3,99*10-7 |
0,32 |
|
|
Lower general secondary |
-0,72 |
0,24 |
9,17 |
1 |
0,002 |
0,49 |
|
|
Medium general secondary |
-0,53 |
0,32 |
2,73 |
1 |
0,099 |
0,59 |
|
|
Upper general secondary |
-0,44 |
0,34 |
1,68 |
1 |
0,195 |
0,64 |
|
|
Intermediate vocational |
-0,76 |
0,22 |
11,82 |
1 |
0,001 |
0,47 |
|
|
Higher vocational |
-0,38 |
0,22 |
3,10 |
1 |
0,078 |
0,68 |
|
|
University or postgraduate |
0 |
. |
. |
0 |
. |
. |
|
Financial balance |
Respondent gives more |
-0,93 |
0,47 |
3,87 |
1 |
0,049 |
0,39 |
|
|
More or less equal |
-0,54 |
0,46 |
1,39 |
1 |
0,238 |
0,58 |
|
|
Other gives more |
0,00 |
. |
. |
0 |
. |
. |
|
Initiative contact |
Usually my initiative |
0,00 |
0,25 |
0,00 |
1 |
0,996 |
1,00 |
|
|
More or less equal |
0,27 |
0,24 |
1,31 |
1 |
0,253 |
1,31 |
|
|
Usually other's initiative |
0 |
. |
. |
0 |
. |
. |
|
Conflict |
Not at all |
1,52 |
0,41 |
13,55 |
1 |
2,33*10-4 |
4,59 |
|
|
Once or twice |
1,92 |
0,47 |
16,43 |
1 |
5,05*10-4 |
6,84 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Sex |
Female |
0,42 |
0,10 |
16,58 |
1 |
4,66*10-4 |
1,52 |
|
Age |
Age |
0,01 |
0,01 |
2,29 |
1 |
0,130 |
1,01 |
|
Living siblings |
Living siblings |
-0,05 |
0,02 |
6,28 |
1 |
0,012 |
0,95 |
|
Financial help received |
No |
-0,99 |
1,13 |
0,78 |
1 |
0,378 |
0,37 |
|
Financial help given |
No |
-0,14 |
0,66 |
0,05 |
1 |
0,827 |
0,87 |
If we set the reference category to ‘interest given several times but received once or twice’, we can interpret differences between parents and the childless.[28] Childless individuals are 2,11 times less likely than parents to have given no interest at all but received once or twice, instead of have given interest several times but received only once or twice over the past three months (Table 23).[29] This while controlling for other variables in the model. It can also be interpreted as follows: childless individuals are 2,11 times more likely than parents to have given interest several times but received only once or twice, instead of ‘given no interest at all but received once or twice’ over the past three months.
The parameter estimates for other comparisons in this model can be found on the cd-rom. Models with other reference categories can also be found on the cd-rom.
Table 23 : Parameter estimates for interest given none but received once or twice (versus interest given several times but received only once or twice)
|
Interest given and received |
None/Once or twice |
λ |
Std. Error |
Wald |
df |
p |
Exp(λ) |
|
|
Intercept |
2,08 |
3,80 |
0,30 |
1 |
0,584 |
|
|
Genetic status sibling |
Full sibling |
0,17 |
0,60 |
0,08 |
1 |
0,775 |
1,19 |
|
Age difference |
Age difference |
0,02 |
0,02 |
0,80 |
1 |
0,371 |
1,02 |
|
Sex sibling |
Female |
-0,22 |
0,17 |
1,65 |
1 |
0,199 |
0,80 |
|
Childless |
Childless |
-0,75 |
0,27 |
7,72 |
1 |
0,005 |
0,47 |
|
Education |
Incomplete/primary |
0,59 |
0,40 |
2,17 |
1 |
0,141 |
1,80 |
|
|
Lower vocational |
0,32 |
0,37 |
0,73 |
1 |
0,392 |
1,37 |
|
|
Lower general secondary |
0,53 |
0,38 |
1,94 |
1 |
0,163 |
1,71 |
|
|
Medium general secondary |
0,32 |
0,52 |
0,38 |
1 |
0,539 |
1,37 |
|
|
Upper general secondary |
0,49 |
0,64 |
0,59 |
1 |
0,441 |
1,64 |
|
|
Intermediate vocational |
0,39 |
0,36 |
1,14 |
1 |
0,286 |
1,47 |
|
|
Higher vocational |
-0,33 |
0,36 |
0,83 |
1 |
0,362 |
0,72 |
|
|
University or postgraduate |
0 |
. |
. |
0 |
. |
. |
|
Financial balance |
Respondent gives more |
-0,89 |
0,76 |
1,38 |
1 |
0,240 |
0,41 |
|
|
More or less equal |
-0,21 |
0,72 |
0,08 |
1 |
0,773 |
0,81 |
|
|
Other gives more |
0,00 |
. |
. |
0 |
. |
. |
|
Initiative contact |
Usually my initiative |
-0,45 |
0,43 |
1,08 |
1 |
0,300 |
0,64 |
|
|
More or less equal |
-0,57 |
0,40 |
1,99 |
1 |
0,159 |
0,57 |
|
|
Usually other's initiative |
0 |
. |
. |
0 |
. |
. |
|
Conflict |
Not at all |
0,42 |
0,83 |
0,25 |
1 |
0,614 |
1,52 |
|
|
Once or twice |
0,00 |
0,92 |
0,00 |
1 |
0,996 |
1,00 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Sex |
Female |
-0,88 |
0,18 |
24,47 |
1 |
7,53*10-7 |
0,41 |
|
Age |
Age |
0,00 |
0,01 |
0,15 |
1 |
0,694 |
1,00 |
|
Living siblings |
Living siblings |
0,05 |
0,04 |
1,59 |
1 |
0,207 |
1,05 |
|
Financial help received |
No |
-0,49 |
1,43 |
0,12 |
1 |
0,731 |
0,61 |
|
Financial help given |
No |
-0,11 |
0,93 |
0,01 |
1 |
0,909 |
0,90 |
7.4.4 Initiative contact
The model has a Nagelkerke R² of 0,25 (-2LL= 5315,47; χ²= 928,85; df=22; p<0,001). Childlessness of sibling, education, age, age difference, interest given and financial help received were not significant predictors of initiative of contact. There appears to be no symmetrical effect for childlessness, sibling childlessness is not significant. Genetic relatedness does not appear to (independently) influence who takes initiative.
Table 24 : Likelihood ratio tests for model for initiative contact
|
Effect |
-2 LL |
χ² |
df |
p |
|
Intercept |
5315,47 |
0 |
0 |
. |
|
Conflict |
5326,25 |
10,79 |
4 |
0,029 |
|
Sex |
5334,39 |
18,93 |
2 |
7,76*10-5 |
|
Sex sibling |
5333,59 |
18,13 |
2 |
1,16*10-4 |
|
Living siblings |
5323,49 |
8,03 |
2 |
0,018 |
|
Financial help given |
5322,33 |
6,86 |
2 |
0,032 |
|
Childlessness |
5323,18 |
7,72 |
2 |
0,021 |
|
Interest received |
5413,29 |
97,82 |
4 |
2,86*10-20 |
|
Financial balance |
5919,14 |
603,67 |
4 |
2,49*10-129 |
Childless individuals are 1,53 times more likely than ‘parents’ to state the other takes initiative, instead of equal initiative, while controlling for other variables (Table 25). Yet, there is no symmetrical effect for childlessness. Childlessness of the sibling does not affect who takes initiative of contact. Moreover, childless respondents are not significantly more likely to report that initiative is equal instead of theirs. Therefore, it is possible that childless individuals report that the other takes more initiative while this is factually untrue. This is what our analysis of ‘giving and receiving interest’ appears to indicate. Childless individuals are more likely than parents to have given interest several times over the past three months while only receiving interest once or twice. This would suggest that childless individuals are more likely to show initiative of contact than parents, unless initiative of contact is not accurately captured by interest given and interest received over the past three months.
Table 25 : Parameter estimates for ‘initiative other’ (versus ‘equal’)
|
Initiative contact: |
Initiative other |
λ |
Std. Error |
Wald |
df |
p |
Exp(λ) |
|
|
Intercept |
1,89 |
1,03 |
3,35 |
1 |
0,067 |
|
|
Conflict |
Not at all |
-0,96 |
0,47 |
4,10 |
1 |
0,043 |
0,38 |
|
|
Once or twice |
-0,29 |
0,52 |
0,31 |
1 |
0,580 |
0,75 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Sex |
Female |
-0,51 |
0,14 |
13,28 |
1 |
2,69*10-4 |
0,60 |
|
Sex sibling |
Female |
0,39 |
0,14 |
7,43 |
1 |
0,006 |
1,47 |
|
Living siblings |
Living siblings |
-0,09 |
0,03 |
6,97 |
1 |
0,008 |
0,91 |
|
Financial help given |
No |
-1,05 |
0,42 |
6,36 |
1 |
0,012 |
0,35 |
|
Childlessness |
Childless |
0,42 |
0,16 |
6,86 |
1 |
0,009 |
1,53 |
|
Interest received |
Not at all |
0,14 |
0,18 |
0,61 |
1 |
0,434 |
1,15 |
|
|
Once or twice |
-0,17 |
0,16 |
1,04 |
1 |
0,308 |
0,85 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Financial balance |
Respondent gives more |
-0,99 |
0,31 |
10,16 |
1 |
0,001 |
0,37 |
|
|
More or less equal |
-1,83 |
0,25 |
52,88 |
1 |
3,54*10-13 |
0,16 |
|
|
Other gives more |
0 |
. |
. |
0 |
. |
. |
7.4.5 Financial balance
The model has a Nagelkerke R² of 0,30 (-2LL= 3682,89; χ²= 2557,36; df=28; p<0,001; Table 26). Sibling childlessness, education, genetic relatedness, initiative contact, age, age difference, sex, sex sibling a and financial help given were not significant (independent) predictors of financial balance. Genetic relatedness does not appear to (independently) affect the financial balance of the relationship.
Table 26 : Likelihood ratio tests for model for financial balance
|
Effect |
-2 LL |
χ² |
df |
p |
|
Intercept |
3682,88 |
0,00 |
0 |
. |
|
Initiative contact |
4288,98 |
606,10 |
4 |
7,42*10-130 |
|
Conflict |
3755,71 |
72,82 |
4 |
5,75*10-15 |
|
Living siblings |
3690,32 |
7,44 |
2 |
0,024 |
|
Financial help received |
3691,93 |
9,04 |
2 |
0,011 |
|
Childlessness |
3696,42 |
13,53 |
2 |
0,001 |
|
Interest given |
3707,30 |
24,42 |
4 |
6,59*10-5 |
|
Interest received |
3749,70 |
66,82 |
4 |
1,07*10-13 |
Childless individuals are 2,44 times more likely than ‘parents’ to state that their sibling gives more, instead of ‘I give more’, while controlling for other variables (Table 27). This is contrary to our prediction, i.e. that childless individuals would give more than parents or have an equal relationship. Yet it could be possible that childless individuals evaluate their (financial) relationship more positively than ‘parents’ and therefore state that the other gives more while this is factually untrue. Another possibility is that childless individuals do in fact have a relationship where the other gives more. Childless individuals cannot rely on their mature children for financial support, whereas parents can. As such as they grow older, they could be a ‘sink hole’ rather than ‘asset’ in terms of inclusive fitness. Yet we did not find a symmetrical effect in terms of childlessness, sibling childlessness does not (independently) influence the financial balance of the relationship. The lack of a symmetrical effect could mean that it is more likely that childless individuals perceive that the other gives more, rather than that childless individuals actually do give more. The parameter estimates for ‘balanced relationship’ versus ‘anchor gives more’ can be found on the cd-rom.
Table 27 : Parameter estimates for ‘other gives more’ (versus ‘anchor gives more’)
|
Financial balance: |
Other gives more |
λ |
Std. Error |
Wald |
df |
p |
Exp(λ) |
|
|
Intercept |
3,33 |
2,85 |
1,36 |
1 |
0,24 |
|
|
Initiative contact |
Usually my initiative |
-3,01 |
0,39 |
58,56 |
1 |
1,97*10-14 |
0,05 |
|
|
More or less equal |
-1,04 |
0,31 |
11,43 |
1 |
7,21*10-4 |
0,35 |
|
|
Usually other's initiative |
0 |
. |
. |
0 |
. |
. |
|
Conflict |
Not at all |
1,08 |
1,05 |
1,05 |
1 |
0,306 |
2,93 |
|
|
Once or twice |
0,54 |
1,10 |
0,24 |
1 |
0,628 |
1,71 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Living siblings |
Living siblings |
0,09 |
0,05 |
2,92 |
1 |
0,088 |
1,09 |
|
Financial help received |
No |
-2,70 |
1,32 |
4,22 |
1 |
0,040 |
0,07 |
|
Childlessness |
Childless |
0,89 |
0,25 |
13,20 |
1 |
2,79*10-4 |
2,44 |
|
Interest given |
Not at all |
0,61 |
0,41 |
2,23 |
1 |
0,135 |
1,84 |
|
|
Once or twice |
0,84 |
0,28 |
9,26 |
1 |
0,002 |
2,31 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
|
Interest received |
Not at all |
-2,15 |
0,41 |
27,79 |
1 |
1,35*10-7 |
0,12 |
|
|
Once or twice |
-1,47 |
0,30 |
24,40 |
1 |
7,82*10-7 |
0,23 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
7.4.6 Giving financial help
It should be noted that the occurrence of giving financial help to a sibling was very low (less than 2%).[30] The model for giving financial help has a Nagelkerke R² of 0,08 (-2LL= 535,43; χ²= 44,77; df=6; p<0,001), it therefore has quite low explanatory value. Sibling childlessness, education, genetic relatedness, interest received, conflict, financial balance age, age difference, sex, sex sibling a and financial help received were not significant (independent) predictors of whether or not financial help was given. Genetic relatedness does not appear to independently influence whether or not financial help was given to a sibling.
Table 28 : Likelihood ratio tests for model for giving financial help
|
Effect |
-2 LL |
χ² |
df |
p |
|
Intercept |
535,43 |
0,00 |
0 |
. |
|
Living siblings |
541,33 |
5,90 |
1 |
0,015 |
|
Childlessness |
545,75 |
10,32 |
1 |
0,001 |
|
Interest given |
549,88 |
14,45 |
2 |
0,001 |
|
Initiative contact |
543,99 |
8,56 |
2 |
0,014 |
Childless individuals are 2,62 times more likely than ‘parents’ to have given financial help to their sibling (Table 29).[31] This while controlling for the other variables.
Table 29 : Parameter estimates for giving financial help (versus ‘not giving financial help’)
|
Financial help: |
Yes |
λ |
Std. Error |
Wald |
df |
p |
Exp(λ) |
|
|
Intercept |
-3,66 |
0,60 |
37,19 |
1 |
1,07*10-9 |
|
|
Living siblings |
Living siblings |
-0,19 |
0,08 |
5,00 |
1 |
0,025 |
0,83 |
|
Childless |
Childless |
0,96 |
0,29 |
11,34 |
1 |
7,58*10-4 |
2,62 |
|
Interest given |
Not at all |
-1,11 |
0,42 |
7,00 |
1 |
0,008 |
0,33 |
|
|
Once or twice |
-1,05 |
0,34 |
9,57 |
1 |
0,002 |
0,35 |
|
|
Several times |
0,00 |
. |
. |
0 |
. |
. |
|
Initiative contact |
Usually my Initiative |
-0,53 |
0,44 |
1,40 |
1 |
0,236 |
0,59 |
|
|
More or less equal |
-1,15 |
0,41 |
7,89 |
1 |
0,005 |
0,32 |
|
|
Usually other's initiative |
0,00 |
. |
. |
0 |
. |
. |
7.4.7 Receiving financial help
As with giving financial help, it should be noted that the occurrence of receiving financial help from a sibling was very low (less than 1%).[32] The model for receiving financial help has a Nagelkerke R² of 0,08 (-2LL= 374,06; χ²= 32,51; df=6; p<0,001). No significant (independent) effects were found for genetic relatedness, sex, sex sibling a, education, age, conflict, financial balance, initiative of contact, giving financial help and giving interest. Genetic relatedness does not appear to (independently) significantly influence the likelihood of receiving financial help.
Table 30 : Likelihood ratio tests for model for receiving financial help
|
Effect |
-2 LL |
χ² |
df |
p |
|
Intercept |
374,06 |
0 |
0 |
. |
|
Age difference |
378,55 |
4,49 |
1 |
0,034 |
|
Childlessness of sibling |
378,04 |
3,98 |
1 |
0,046 |
|
Living siblings |
380,12 |
6,06 |
1 |
0,014 |
|
Childlessness |
379,57 |
5,51 |
1 |
0,019 |
|
Interest received |
384,27 |
10,22 |
2 |
0,006 |
Respondents are 2,14 times more likely to receive financial help from a childless sibling than from a sibling who has children. Yet, childless individuals are 2,41 times more likely to receive financial help than parents. This appears inconsistent with our predictions.
Table 31 : Parameter estimates for receiving financial help (versus ‘not receiving financial help’)
|
Financial help: |
Yes |
λ |
Std. Error |
Wald |
df |
p |
Exp(λ) |
|
|
Intercept |
-5,38 |
0,63 |
72,35 |
1 |
1,80*10-17 |
|
|
Age difference |
Age difference |
0,08 |
0,03 |
5,31 |
1 |
0,021 |
1,08 |
|
Sibling childlessness |
Childless |
0,76 |
0,36 |
4,36 |
1 |
0,037 |
2,14 |
|
Living siblings |
Living siblings |
-0,23 |
0,10 |
5,00 |
1 |
0,025 |
0,79 |
|
Childless |
Childless |
0,88 |
0,36 |
6,04 |
1 |
0,014 |
2,41 |
|
Interest received |
Not at all |
-0,99 |
0,47 |
4,46 |
1 |
0,035 |
0,37 |
|
|
Once or twice |
-1,21 |
0,46 |
6,89 |
1 |
0,009 |
0,30 |
|
|
Several times |
0 |
. |
. |
0 |
. |
. |
7.4.8 Giving and/or receiving financial help
Through combination of ‘giving’ and ‘receiving’ financial help we can investigate whether or not relationships are symmetric or asymmetric, in terms of actual financial help over the past twelve months. As we already mentioned, in the majority of the cases no money or valuables were given or received in the past twelve months. From the analyses presented above (7.4.6 and 7.4.7), it can also be derived that most financial relationships are not symmetrical. Receiving money or valuables is not a significant predictor for giving money or valuables and vice versa.
Yet, there appear to be small differences between childless individuals and parents. At first sight, childless individuals seem to be giving but not receiving (very) slightly more often. Unfortunately, only MLR-models for which the parameter estimates are uncertain can be constructed, these can be found on the cd-rom.
If we assume that the graphs presented below are an accurate reflection of the ‘financial balance’ of the sibling relationship, childless individuals have marginally more unbalanced financial relationships, in which they give but do not receive (Figure 8 to figure 10). Unless the financial balance of the relationship is not captured in this twelve months time frame, the graphs appear to indicate that it is the childless individual’s perception that the other gives more, rather than that there is an actual imbalance. Yet, we should take into account that we are dealing with only a very small number of cases in which money or valuables were given and/or received.
Figure 8 : Childlessness and giving and receiving financial help
Figure 9 : Childlessness and giving and receiving financial help (detail)
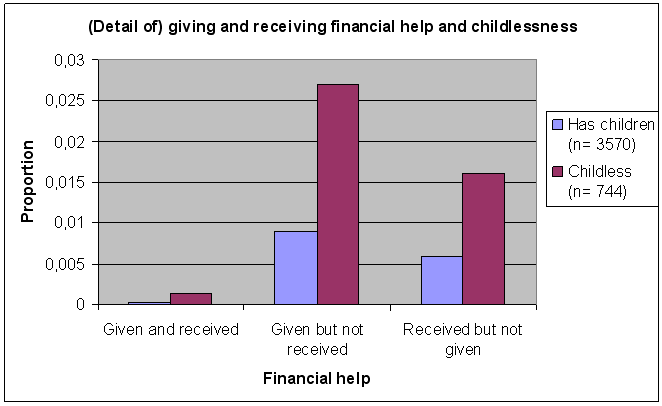
Figure 10 : Childlessness and giving and receiving financial help (if help occurs)
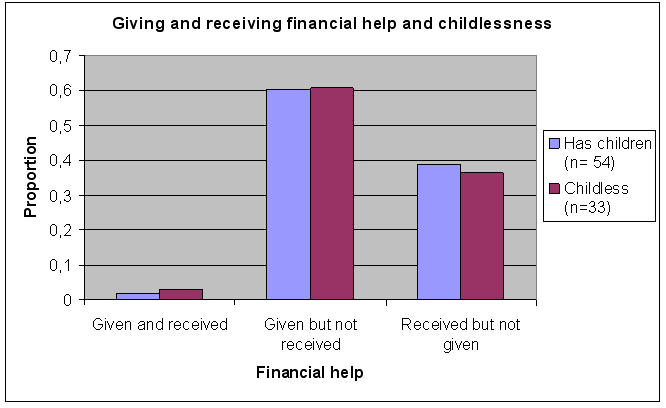
If we investigate only the cases in which a ‘financial transfer’ did actually occur, we find no significant differences between childless individuals and parents (χ²= 0,164; df= 2; p= 0,923; Figure 10). In the majority of all occurrences, money or valuables were given but not received over the past twelve months. If the financial transfers over the past twelve months are an accurate reflection of the financial balance between the siblings, childless individuals do not significantly receive more than they give. This would indicate that the results found for ‘financial balance’ are possibly due to the perception of childless individuals rather than that they in fact receive more from their sibling, provided that the financial balance of the relationship is captured by the financial relationships over the past twelve months.
7.5 Voluntary and involuntary childlessness and sibling relationships
The analyses presented so far did not distinguish between voluntary childless (‘childfree’) and involuntary childless respondents. Unfortunately, only 285 respondents responded to the question: ‘Do you consider yourself to be voluntarily childless or would you have liked to have had children?’ (Dykstra et al., 2004). Answer categories were ‘voluntarily childless’ (1) or ‘would have liked to have had children’ (2). The question was only asked to women aged forty or over and men aged forty five or over.
There are no significant differences between the childfree and the involuntary childless in terms of gender (r= -0,53; p= 0,37; Figure 11).
Figure 11 : Gender and voluntary or involuntary childlessness
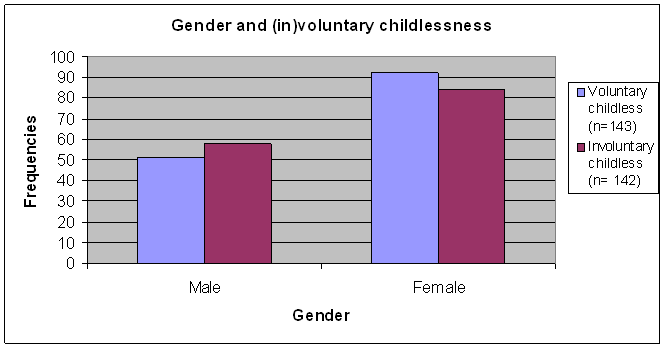
As can be expected by individualization theory, higher educated individuals are significantly more childless by choice than lower educated individuals (Somers’ Dyx= -0,11; p= 0,009; Figure 12). The voluntary childless are also significantly younger than the involuntary childless (r= 0,15; p= 0,01; Figure 13). This could be explained by the fact that later born respondents had more medical technologies to their aid, which would help avoid involuntary childlessness. Moreover, the increasing rate of voluntary childlessness is a rather recent trend (2.2).
Figure 12 : Education and (in)voluntary childlessness
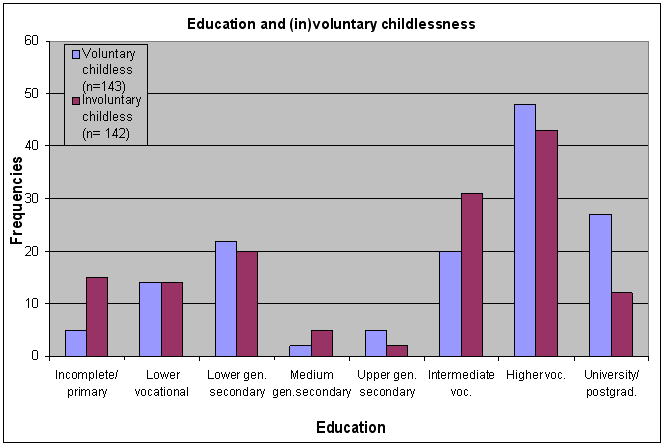
Figure 13 : Age and (in)voluntary childlessness
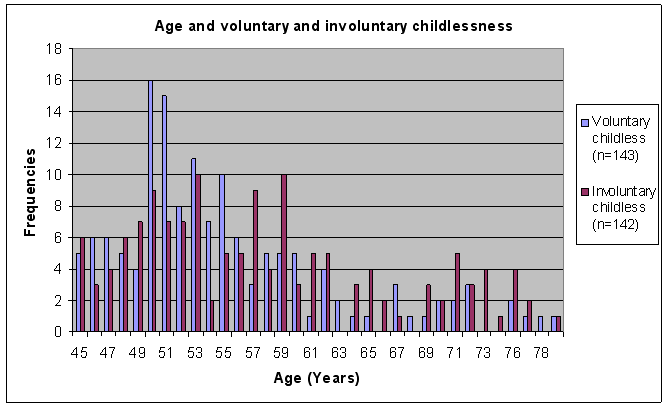
Intuitively, we would expect that involuntary childless respondents are more likely to ‘invest’ in kin relations and more likely to maintain higher quality relationships with their kin than childfree respondents. Involuntary childless individuals do indeed have (significantly) better relationships with their sibling than childfree individuals (Mann-Whitney U= 7455; one-tailed p= 0,022; Figure 14).
Figure 14 : Involuntary and voluntary childlessness and quality of relationship with sibling
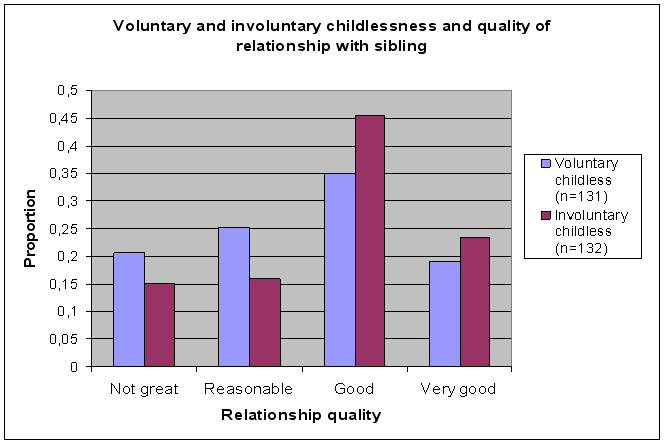
Yet, there are no significant differences between involuntary childless and childfree respondents for other relationships aspects such as ‘initiative of contact’ (Mann-Whitney U= 65144; one-tailed p= 0,341), ‘financial balance’ (Mann-Whitney U= 6714,5; one-tailed p= 0,434), ‘giving interest’ (Mann-Whitney U= 6533,5; one-tailed p= 0,306) and ‘giving financial help’ (χ² with Yates correction; one-tailed p= 0,427) (Figure 16 to figure 19 in appendix). In addition, there are no significant differences between ‘childfree’ respondents and involuntary childless respondents in terms of ‘receiving financial help’ (χ² with Yates correction; p= 0,499), ‘interest received’ (Mann-Whitney U= 6428; p= 0,469) and ‘conflict’ (Mann-Whitney U= 6703,5; p= 0,789) (see cd-rom).
If we select only the individuals for whom ‘sibling a’ has a child, our conclusions remain the same. Involuntary childless individuals have a better relationship with their sibling than childfree individuals (Mann-Whitney U= 4049; one-tailed p= 0,004; Figure 15). Yet, there are no significant differences between involuntary childless and childfree respondents in terms of other discussed relationship aspects (at α= 0,05; see cd-rom).[33]
Figure 15 : Involuntary and voluntary childlessness and relationship quality with a sibling who has children
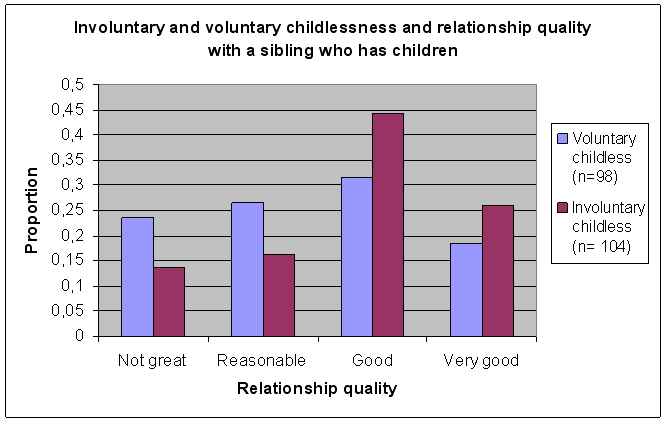
8. General discussion and limitations of the study
8.1 General discussion
Preliminary (descriptive) analyses indicated that genetic relatedness affects relationship quality and interest given and received (Figure 1, Figure 2, Figure 4). Also, childless individuals appear more likely than ‘parents’ to have a very good relationship, in which interest is given and received several times over the past three months, instead of a good relationship (Figure 3). The homogeneity analysis by alternating least squares indicated that the difference between parents and childless individuals lies between a ‘good’ and ‘very good’ relationship.
Except for sibling childlessness, gender of sibling, genetic relatedness and age difference, the variables proposed are significant predictors of relationship quality in a MLR-model (Table 3). As the HOMALS for ‘childlessness’, ‘interest’ and ‘relationship quality’ indicated that the differences between the childless and parents is centred upon ‘good’ versus ‘very good’, the reference category for the MLR was set to ‘good’. In general, the direction of the parameter estimates was consistent with our predictions (Table 14; cd-rom). The initial model had a (very) good Nagelkerke R² and was only marginally improved by inclusion of two-way interaction variables. None of the two-way interaction effects with genetic relatedness or childlessness improved the model significantly.
As predicted, social factors, for instance interest, were (very) strong predictors of relationship quality in the MLR-model. While controlling for such social and other factors, e.g. education, our analyses showed that childless individuals are significantly more likely than ‘parents’ to maintain high quality relationships with their siblings. Childless individuals are approximately one and a half time more likely than parents to have a very good relationship instead of a good relationship, while controlling for a wide range of social and other variables (Table 5). Furthermore, high quality sibling relationships appear to require some (mutual) ‘investments’. Giving and receiving interest in one’s personal life and giving money or valuables strongly affect the quality of the relationship. It is important to note that we found an effect for childlessness on relationship quality while controlling for these investment measures. Therefore, the effect found for childlessness cannot be attributed to social aspects of the relationship, e.g. receiving financial help.
Following individualization theory, there is no apparent reason why childless individuals should maintain stronger relationships with their siblings than parents. Yet, the finding that childless individuals maintain high quality relationships with their siblings is consistent with our predictions derived from an inclusive fitness point of view. It is possible that these high quality relationships with their siblings yield some inclusive benefits for childless individuals. Studies of human social networks show that the number of high quality relationships is restricted (4). Therefore relationship quality of one relationship is traded off against other relationships. As childless individuals do not have to trade off kin relations against relationships with their children, they are able to maintain higher quality relationships with their siblings than parents. Differences between childless individuals and parents in quality of relationship with their sibling seem consistent with an inclusive fitness point of view.
A possible alternative, yet not necessarily mutually exclusive, explanation for differences between parents and the childless in quality of relationship is that these high quality relationships act as a ‘buffer’ against social isolation of childless individuals when they reach old age. Whereas individuals with children can rely on their children for social in support in old age, childless individuals could rely on their siblings and their offspring (see, Wenger, 1992/1997; Wenger et al., 2000). In order to avoid social isolation in old age childless individuals invest more in relationships with their sibling (and of course their nieces and nephews) than parents. As we selected individuals aged forty of over, this might increase the possibility of such an effect. However, we note that we found the effect for childlessness on relationship quality while controlling for age.
Although we initially found no (independent) effect for genetic relatedness on relationship quality, this can be explained by the strong predictive value of other variables in the model. If we omit certain variables (education, full living siblings and interest received) with which genetic relatedness correlates from the model, we find a significant independent effect of genetic relatedness on relationship quality. This MLR-model still performs well according to standards in the social sciences. In this alternative model, respondents are significantly more likely to have a good or very good relationship, instead of a not great relationship, with a full sibling than with an adopted or half-sibling. Respondents were nearly two and a half times more likely to have a good relationship instead of a not great relationship with their sibling, if they were fully related to them. If their sibling is a full sibling, respondents are 2,75 times more likely to have a very good instead of a not great relationship compared to when they are not fully related with their sibling. Both effects were found while controlling for various social factors (interest given, financial help, financial balance, initiative of contact, conflict) and other factors (e.g. age) in the model (Table 11). However, if we attempt to control for education, full living siblings or interest received we find no (independent) effect for genetic relatedness. Unfortunately, the number of adopted siblings in the sample is quite low; therefore we decided to merge the categories of half-siblings and adopted siblings. Our analyses did thus not distinguish for effects between adopted (r=0) and half-siblings (r=0,25).
There was also no (independent) effect of sibling childlessness on quality of relationship in the initial model. This could be attributed to the fact that the question on relationship quality was asked to the ‘anchor’ and not to the sibling. However, there is some indication that childless individuals have a better relationship with their sibling if their sibling has children (Figure 5).
An analysis of ‘investment’ measures (interest, initiative of contact, financial balance and financial help) shows some interesting results. As could be expected, social factors are strong predictors of these ‘investment measures’. Therefore, while attempting to control for such factors, it is possible that we do not find significant (independent) effects for childlessness and genetic relatedness. Moreover, it should be noted that the models for financial help performed poorly in terms of Nagelkerke R² (7.4.6 and 7.4.7).
Childless individuals show more interest in their sibling’s personal life than ‘parents’, this while controlling for several factors (Table 16). Childless respondents are 1,36 times more likely to have shown interest several times, instead of not at all, in their sibling’s personal life over the past three months. However, if we attempt to control for interest received, there is no significant (independent) effect for childlessness.
Childless individuals are not significantly more likely than parents to receive interest in their personal life. However, contrary to our predictions, respondents are more likely to have received interest in their personal life from a sibling who has children than from a childless sibling. This is in contrast with the findings for ‘interest’ given. It is unclear how to reconcile both findings. The finding that respondents received significantly more interest in their personal life than from a sibling who has children than from a childless sibling could possibly be attributed to a more positive evaluation of individuals with children (see Somers, 1993; 2.2). The difference in perspective, given versus received, could also influence the differential findings.
Childless individuals are significantly more likely to have an asymmetrical relationship with their sibling, in which they show interest in their sibling’s personal life several times but receive interest only once or twice. For childless respondents, approximately one third of the dyads can be characterized by interest shown in sibling’s personal life several times, but ‘received interest only once or twice’ (over the past three months). Childless individuals are 2,11 times more likely than parents to have given interest several times in their sibling’s personal life while receiving interest only once or twice, compared to ‘interest given none but received once or twice’. This effect was found while controlling for other (Table 23). However sibling childlessness did not independently influence interest given and received. This is contrary to our expectations but this could be due to the fact that the survey asked questions to the respondent, rather than to the sibling.
Childless individuals indicate that the other shows (significantly) more initiative to contact them, rather than there is a balance in ‘initiative of contact’. Yet, one could ask whether this is factually true, given that childless individuals are significantly more likely to have an asymmetrical relationship in terms of interest given and received.[34] Over the past three months, childless individuals were significantly more likely to have given interest in the other’s personal life several times, while receiving interest only once or twice. If we assume the last three months are an accurate reflection of ‘initiative of contact’, it could be that childless respondents gave social desirable answers on this item. Moreover sibling childlessness was not a significant (independent) predictor of initiative of contact.
Childless individuals are more likely to give and receive a large amount of money or valuables. These findings are similar to the findings by Essock-Vitale and McGuire (1985), who found that childless respondents were more likely to give to and receive help from nieces and nephews. Respondents are also more likely to receive financial help from a childless sibling than from a sibling who has children. If financial transfers between siblings did occur, the majority of them can be characterized as ‘given but not received’. There were no significant differences between parents and childless respondents in terms of symmetry, if a financial transfer did occur. Yet, we should bear in mind that the occurrence of financial help (given and received) was very low. In less than three percent of the cases the respondent has given to or received financial help from their sibling over the past twelve months.
Childless individuals are more likely than ‘parents’ to state that they receive more from their siblings, rather than have an equal relationship. This is contrary to our expectations, i.e. that childless individuals would have a balanced relationship or give more to their sibling than ‘parents’. Yet, if we look at actual financial relationships over the past twelve months, we do not find that childless individuals are significantly more likely to receive, without haven given. It is possible however, that actual financial relationships over the past twelve months are not an accurate reflection of the ‘financial balance’ of the sibling relationships. Childless individuals may have given social desirable answers, or their positive evaluation of the relationship with their sibling could have led them to answer that ‘the other gives more’, while this is factually untrue. Moreover, it should be noted that sibling childlessness was not a significant predictor for ‘financial balance’.
In conclusion, there is mixed evidence that childless individuals invest more in their relationship with their sibling than parents. It is possible that the lack of straightforward evidence for significant differences in financial and social ‘investment’ between childless individuals and parents is due to the selection of individuals aged over forty. As their siblings are aged forty or over, the nieces and nephews of respondents are likely to have reached an age at which they are self-sufficient. Therefore, we conclude there is some evidence that childless individuals invest more in their sibling relationships than parents but further study is necessary.
As can be derived from inclusive fitness theory, more distantly related individuals interact less than closely related individuals. Full siblings were found to interact more than adopted or half-siblings. Respondents are significantly more likely to have received interest in their personal life (over the past three months) from a full sibling than from a half-sibling or an adopted sibling, this while controlling for a wide range of other variables (Table 18). In approximately four out of ten relationships where the siblings are not fully related, the respondents have not received any interest in their personal life over the past three months. Individuals are also significantly more likely to have shown interest in a full sibling’s personal life than in an adopted or half-sibling’s personal life. However, if we control for ‘interest received’, we find no significant (independent) effect for genetic relatedness on ‘interest given’. Approximately one quarter of the dyads where the siblings are not fully related can be characterized by ‘no interest given and received’ over the past three months at all. Full siblings are 2,25 more likely than not fully related siblings to have a relationship in which interest was given and received once or twice over the past three months, instead of ‘not given and received at all’, while controlling for a wide range of variables (Table 22). Thus, we conclude that genetic relatedness (strongly) affects social investment in relationships. Rather than merely being influenced by ‘individualized choice’ as claimed by modernization theories (1), sibling relationships are affected by genetic relatedness.
Genetic relatedness did not appear to (independently) affect other aspects of the sibling relationship (giving/receiving financial help, financial balance and initiative of contact). However, several of these relationship aspects are determined by giving and/or receiving interest. For instance, as adopted or half-siblings interact less, they are less likely to have given money. Therefore, there is possibly still an indirect effect of genetic relatedness on these relationship aspects. These direct and indirect effects of genetic relatedness could be further explored by a logistic path model or by structural equation modelling.
In conclusion, genetic relatedness affects social investment, i.e. giving and receiving interest, as well as quality of sibling relationships. Yet further research is necessary to investigate the direct and indirect effects of genetic relatedness on sibling relationship characteristics.
The multinomial logistic analyses presented so far did not distinguish between ‘childfree’ and involuntary childless respondents. The NKPS survey does ask individuals whether they are childless by choice or not (Dykstra et al., 2004). Unfortunately, only 285 respondents answered to this question. As predicted by individualization theory and found in previous studies, e.g. McAllister and Clarke (1998) and Bachu (1999), childfree individuals are predominantly higher educated. Childfree individuals are also significantly younger than the involuntary childless. Involuntary childless individuals were found to have a significantly better relationship with their sibling than childfree individuals. This is consistent with the idea that ‘individualized choice of childlessness’ affects sibling relationships. If we selected only siblings who had children, involuntary childless were also significantly closer with their sibling than childfree individuals. There were no significant differences between childfree and involuntary childless individuals in terms of other aspects of the relationship or investment, e.g. financial balance. This might be due to the fact that their siblings have children who are self-sufficient.
Yet, it is important to bear in mind that, as other studies have shown, the majority of the childless are childless by choice rather than involuntary childless (see 2.2). Therefore it is unlikely that the effects found for ‘childlessness’ in the models for sibling relationship quality and ‘investments’ can be attributed solely to the involuntary childless.
In conclusion, we have summarized the most important findings relating to inclusive fitness theory in the table below.
Table 32 : Main findings
|
|
CHILDLESSNESS |
|
|
|
|
1 |
Childless individuals have significantly better relationships with their siblings |
|
|
than parents. These relationships are characterized by (mutual) investments. |
|
|
This is consistent with the view that childless individuals do not have to trade |
|
|
off relationships with offspring against kin relations. |
|
|
|
|
|
|
|
2 |
There is mixed evidence that childless individuals invest more in their sibling |
|
|
relationship than parents, in terms of time and money. Childless individuals |
|
|
are more likely than parents to have shown interest in their sibling's personal |
|
|
life several times, while receiving interest only once or twice (over the past |
|
|
three months), for instance. |
|
|
|
|
|
GENETIC RELATEDNESS |
|
|
|
|
3 |
Individuals have significantly better relationships with a full sibling than with |
|
|
a sibling to whom they are not fully related. (However, if we control for certain |
|
|
variables we find no effect). |
|
|
|
|
|
|
|
4 |
Individuals show more social investment in relationships with a full sibling |
|
|
than in relationships with an adopted or half-sibling. (Yet genetic relatedness |
|
|
did not independently affect other relationship aspects, e.g. financial help.) |
|
|
|
8.2 Limitations and further research
One of the drawbacks of the analyses for quality of relationship with a sibling is that there were only four categories. A ten point scale, for instance, would allow a better understanding of the differences between childless individuals and parents in relationship quality. A working paper included on the cd-rom, examining the effects of childlessness on relationships with nieces/nephews, uses a ten point scale to examine relationship quality.
Moreover, our study is unable to determine the actual inclusive fitness consequences of the ‘stronger relationships’ that childless individuals have. The studied dataset contains no data which allow investigating the effects of childlessness on relationships with nieces and nephews. However, a preliminary investigation of this type with a different dataset can be found on the cd-rom. Moreover, our analyses lack full data on the entire social network. Such data would allow to look at differences between childless individuals and parents in trade-offs of kin and social relationships. This would allow to confirm that it is trade-offs between relationships with children and kin that lead to differences in sibling relationship quality between childless individuals and parents.
The analyses of quality relationship assumed that social variables, such as interest are predictors of relationships quality. Yet, it can be argued that the causality flows in a different way, i.e. that quality of relationship determines other social determinants, e.g. giving interest, of the sibling relationship. From a social network paradigm (e.g. McPherson et al., 2001), it is more likely that the discussed social variables, such as conflict, are determinants of relationship quality rather than vice versa. Moreover, our primary interest was investigating whether or not childlessness and genetic relatedness influenced relationship quality while controlling for these social variables.
As the NKPS set used here is the first part of a longitudinal design, future waves could allow the study of long term fitness consequences of these relationships. It would allow to select younger respondents who in future waves remain childless. As such, it would allow a more thorough longitudinal analysis of sibling relationships and (possible) fitness consequences.
The ‘investment measures’ we used for the study are not very detailed. The ‘costs’ they present are not necessarily high, e.g. showing interest in the other’s personal life. Future data waves could however discern ‘consistent’ investment, and therefore accumulated costs, over a prolonged period of time.
A longitudinal design could also determine whether or not childless individuals fulfil a helper role, e.g. by providing child-care or financial help. In addition, such a design would allow to investigate whether some of the effects found in this study are due to the selection of respondents aged forty or over.
The study presented here could be further extended by use of structural equation modelling (Loehlin, 2004) or logistic path models (Eshima et al., 2001). This would allow to distinguish between direct and indirect effects of childlessness and genetic relatedness on relationship quality. Further research can also analyze whether the effects found for sibling relationships are specific to these relationships. Do childless individuals have better relationships with their friends, partner, parents and other relatives as well? Are childless individuals and ‘parents’ significantly different in terms of their (overall) social network structure? If the childless have different social network structures, e.g. stronger ties with kin, this could have inclusive fitness consequences. Data on full social network structure would allow a closer examination of differences between childless individuals and ‘parents’ in terms of ‘support cliques’, ‘sympathy groups’ and overall network size. A longitudinal design would allow to investigate differences between ‘the childless’ and parents in social network structures throughout the life course.
In this paper we have shown that childless individuals aged forty or over, are more likely than individuals who have children to have a very good instead of a good relationship with their sibling. This effect was found while controlling for several other predictors of relationship quality. ‘Better relationships’ appear to be characterized by (mutual) ‘investments’ in terms of time and money. The difference between parents and the childless in sibling relationship quality is consistent with the view that childless individuals do not have to trade off relationships with their kin against relationships with their children and are therefore able to maintain stronger relationships with their siblings than parents. It is possible that maintaining stronger relationships with their kin could generate inclusive fitness benefits for childless individuals, even in radicalized modern societies. However, a more thorough longitudinal design is necessary to investigate this claim.
There is mixed evidence that childless individuals ‘invest’ more in their sibling relationships. While controlling for other factors, childless respondents were found to be significantly more likely than parents to have shown an interest in their sibling’s personal life over the past three months. There were no significant differences between childless respondents and parents in the likelihood to have received interest in their personal life from their sibling. However, contrary to our predictions, respondents were more likely to state that they received interest once or twice over the past three months (versus not at all) in their personal life from a sibling who has children, than from a childless sibling.
Childless individuals were found to be significantly more likely than parents to have shown interest in their sibling’s personal life several times over the past three months, while receiving interest only once or twice. Yet, childless individuals were significantly more likely than parents to state that their sibling took initiative to contact them, rather than that both took equal initiative to contact each other. This is in contrast with the finding that childless individuals are significantly more likely than parents to have given interest several times, but have received interest only once or twice. Assuming that ‘interest given and received’ over the past three months is an accurate reflection of initiative of contact, childless individuals are significantly more likely than parents to show initiative to contact their siblings.
Childless individuals were also significantly more likely than parents to give money or valuables to their sibling. Yet, childless individuals were also more likely than parents to receive money. There were no significant differences between parents and the childless in symmetry of giving and receiving money or valuables over the past twelve months. Yet, childless individuals were significantly more likely than ‘parents’ to state that the other gave more to them, rather than that there was an equal relationship between them. There is no evidence for an imbalance, however, if we examine the factual financial relationships over the past twelve months.
There is mixed evidence for more investments by childless individuals than by parents. Further research in a longitudinal design is necessary, however, to thoroughly investigate the effects of childlessness on investment in sibling relationships and the consequences of such investment.
In an alternative model for quality of sibling relationships, respondents were shown to have stronger relationships if they were fully related to their sibling. In addition, siblings were found to significantly interact more if they were fully related instead of being not fully related, while controlling for other variables, e.g. gender or education. These findings are consistent with predictions from inclusive fitness theory. Yet genetic relatedness did not appear to (independently) influence other relationship characteristics, e.g. giving or receiving financial help.
We conclude that childless individuals maintain stronger relations with their siblings than parents. There is at least some evidence that childless individuals invest more in their sibling relations than parents. Yet, further research is necessary to investigate whether and how these stronger relations have consequences for (inclusive) fitness. Moreover, consistent with inclusive fitness theory, genetic relatedness appears to affect (mutual) interest in the personal life of siblings and their relationship quality. Sibling relationships in radicalized modern societies are still strongly affected by other factors besides ‘individualized’ choice, such as genetic relatedness. Inclusive fitness theory can provide a useful framework to explain differences in sibling relationship characteristics. Yet, more research is necessary to investigate the direct and indirect effects of childlessness and genetic relatedness on sibling and other social relationships.
Thomas Pollet (th_pollet@advalvas.be)
- Adams A.M., Madhavan S. & Simon D. (2002). Women's social networks and child survival in Mali, in Social Science and Medicine, 54: 165-178.
- Alam N. (1995). Birth Spacing and Infant and Early Childhood Mortality in a High Fertility Area of Bangladesh: Age-Dependent and Interactive Effects, in Journal of Biosocial Science, 27: 393-404.
- Alcock J. (1998). Animal Behavior: an evolutionary approach, 6th edition, Massachusets: Sinauer.
- Alvard M. (2003). Kinship, lineage and an evolutionary perspective on cooperative hunting in Indonesia, in Human Nature, 14: 129-163.
- Bachu A. (1999) (online). Is Childlessness among American Women on the Rise? Population Division Working Paper No. 37 http://www.census.gov/population/www/documentation/twps0037/twps0037.html (consulted on 19-6-2005).
- Barrett L., Dunbar R.I.M. & Lycett J.E. (2002). Human Evolutionary Psychology, London: Palgrave.
- Beck U. (1993[1992]). The Risk Society, London: Sage.
- Beck U. & Beck-Gernsheim E. (2002). Individualization, London: Sage.
- Beck-Gernsheim E. (2002). Reinventing the Family: In Search of New Lifestyles, Cambridge: Polity Press.
- Becker G. (1991[1981]). A treatise on the family, Cambridge: Harvard University press.
- Belsky J., Steinberg L. & Draper P. (1991). Childhood experience, interpersonal development, and reproductive strategy: an evolutionary theory of socialization, in Child Development, 62: 647-670.
- Bereczkei T. (1998). Kinship network, direct childcare and fertility among Hungarians and Gypsies, in Evolution and Human Behavior, 19: 283-298.
- Berté N.A. (1988). K’ekchi horticultural labor exchange: productive and reproductive implications, in Betzig L., Bogerhoff Mulder M. & Turke P. (eds.). (1988). Human reproductive behaviour: a Darwinian perspective, Cambridge: Cambridge University press, 83-96.
- Betzig L. & Turke P.W. (1986). Food Sharing on Ifaluk, in Current Anthropology, 27: 397-400.
- Blau P.M. (1964). Exchange and Power in Social Life, New York: Wiley.
- Blau P.M. (1977). Inequality and Heterogeneity: A Primitive Theory of Social Structure, New York: Free Press.
- Blau P.M. (1980). A fable about social structure, in Social Forces, 58: 777-788.
- Bove R.B., Vallegia C.R. & Ellison P.T. (2002). Girl helpers and time allocation of nursing women among the Toba of Argentina, in Human Nature, 13: 457-472.
- Bowles S. & Posel D. (2005). Genetic relatedness predicts migrants’ workers remittances to their families, in Nature, 434: 380-383.
- Burnstein E., Crandall C. & Kitayama S. (1994). Some Neo-Darwinian decision rules for altruism: Weighing cues for inclusive fitness as a function of the biological importance of the decision, in Journal of Personality and Social Psychology 67: 733-789.
- Buys C.J. & Larsen K.L. (1979). Human sympathy groups, in Psychological Report, 45: 547-553.
- Callan V.J. (1986). Single women, voluntary childlessness and perceptions about life and marriage, in Journal of Biosocial Science, 18: 479-487.
- Callan V.J. (1987). The Personal and Marital Adjustment of Mothers and of Voluntarily and Involuntarily Childless Wives, in Journal of Marriage and the Family, 49: 847-856.
- Campbell E. (1985). The Childless Marriage: An exploratory study of couples who do not want children, London: Tavistock.
- Cashdan E. (1985). Coping with risk: reciprocity among the Basarwa of Northern Botswana, in Man, 20: 454-474.
- Chagnon N. & Bugos P. jr. (1979). Kinship and social conflict: An analysis of a Yanomamö ax fight in Chagnon N. & Irons W. (eds.) (1979). Evolutionary Biology and Human Behavior, Massachusets: Duxbury Press, 213-238.
- Clausen S.E. (1998). Applied Correspondence Analysis: An Introduction, Quantitative Applications in the Social Sciences Series #121, Thousand Oaks: Sage Publications.
- Cockburn A. (1994). Adaptive sex allocation by brood reduction in antechinuses, in Behavioral Ecology and Sociobiology, 35: 53-62.
- Coleman J. (1990). Foundations of Social Theory, Cambridge: the Belknap press of the Harvard University press.
- Cook K.S. & Whitmeyer J.M. (1992). Two Approaches to Social Structure: Exchange Theory and Network Analysis, in Annual Review of Sociology, 18: 109-127.
- Coon C.S. (1946). The universality of natural groupings in human societies, in Journal of Educational Sociology, 20: 163-168.
- Crognier E., Baali A., & Hilali H.K. (2001). Do “Helpers at the Nest” Increase Their Parents’ Reproductive Success? in American Journal of Human Biology, 13: 365–373.
- Curtis S.L., Diamond I. & McDonald J.W. (1993). Birth interval and family effects on postneonatal mortality in Brazil, in Demography, 30: 33-43.
- Daly M. & Wilson M.I. (1981). Abuse and neglect of children in Evolutionary Perspective, in Alexander R.D. & Tinkle D.W. (1981). Natural selection and social behavior: recent research and new theory, Oxford: Blackwell, 405-417.
- Daly M. & Wilson M.I. (1982). Homicide and kinship, in American Anthropologist, 84: 372-378.
- Daly M. & Wilson M.I. (1985). Child abuse and other risks of not living with both parents, in Ethology and Sociobiology, 6: 197-210.
- Daly M. & Wilson M.I. (1988). Evolutionary social psychology and homicide, in Science, 242: 519-524.
- DeOllos I.Y. & Kapinus C.A. (2002). Aging childless individuals and couples: Suggestions for new directions of research, in Sociological Inquiry, 72: 72-80.
- Dunbar R.I.M. (1993). Coevolution of neocortex size, group size and language in humans, in Behavioral and Brain Sciences, 16: 681-694.
- Dunbar R.I.M. (1998). The social brain hypothesis, in Evolutionary Anthropology, 6: 178-190.
- Dunbar R.I.M. (2004[1996]). Grooming, gossip and the evolution of language, 2nd edition, London: Faber & Faber.
- Dunbar R.I.M. & Spoors M. (1995). Social networks, support cliques and kinship, in Human Nature, 6: 273-290.
- Dunbar R.I.M., Clark A. & Hurst N.L. (1995). Conflict and cooperation amongst Vikings: Contingent behavioural decisions in Ethology and Sociobiology, 16: 233-246.
- Dykstra P.A., Kalmijn M., Knijn T.C.M., Komter A. E., Liefbroer A.C. & Mulder C.H. (2004). Codebook of the Netherlands Kinship Panel Study, a multi-actor, multi-method panel study on solidarity in family relationships, Wave 1. NKPS Working Paper No. 1, The Hague: Netherlands Interdisciplinary Demographic Institute.
- Emlen S.T. (1995). An Evolutionary Theory of the Family, in Proceedings of the National Academy of Science, USA, 92: 8092–8099.
- Eshima N., Tabata M. & Zhi G. (2001). Path analysis with logistic regression models: effect analysis of fully recursive causal systems of categorical variables, in Journal of the Japanese Statistical Society, 31: 1-14.
- Essock-Vitale S.M. & McGuire T.M. (1985). Women’s lives viewed from an evolutionary perspective. II. Patterns of helping, in Ethology and Sociobiology, 6: 155-173.
- Fisher R.A. (1958[1930]). The Genetical Theory of Natural Selection, New York: Dover publications.
- Frank L.G., Glickman S.E., Licht P. (1991). Fatal sibling aggression, precocial development, and androgens in neonatal spotted hyenas, in Science, 252: 702-704.
- Giddens A. (1991). Modernity and Self identity, London: Polity.
- Gillespie R. (2003). Childfree and feminine: understanding the gender identity of voluntary childless women, in Gender and Society, 17: 122-136.
- Grbic M., Ode P.J. & Strand M.R. (1992). Sibling rivalry and brood sex ratios in polyembryonic wasps, in Nature, 360: 254-256.
- Gurven M. (2004). To give or to give not: The behavioural ecology of food transfers, in Behavioral and Brain Sciences, 27: 543-583.
- Gurven M., Hill K., Kaplan H., Hurtado A. & Lyles R. (2000). Food Transfers Among Hiwi Foragers of Venezuela: Tests of Reciprocity, in Human Ecology, 28: 171-218.
- Hames R.D. (1979). Relatedness and Interaction among the Ye’kwana: A Preliminary Analysis, in Chagnon N. & Irons W. (eds.) (1979). Evolutionary Biology and Human Behavior, Massachusets: Duxbury Press, 238–249.
- Hames R.D. (1987). Garden labor exchange the Ye’kwana, in Ethology and Sociobiology, 8: 259-284.
- Hames R.D. & Draper P. (2004). Women’s work, childcare and helpers at the nest in a traditional hunter-gatherer society, in Human Nature, 15: 319-341.
- Hamilton W.D. (1964). The genetical evolution of social behaviour I, II, in Journal of Theoretical Biology, 7: 1-52.
- Hawkes, K., O’Connell J.F. & Blurton Jones N.G. (1997). Hadza Women’s Time Allocation, Offspring Provisioning and the Evolution of Long Postmenopausal Life Spans, in Current Anthropology, 38: 551-578.
- Hill R.A. & Dunbar R.I.M. (2003). Social Network Size in Humans, in Human Nature, 14: 53-72.
- Hobcraft J.N., McDonald J.W. & Rutstein S.O. (1985). Demographic determinants of infant and early child mortality: a comparative analysis, in Population Studies, 39: 363-385.
- Hosmer D. & Lemeshow S. (1989). Applied Logistic Regression, New York: Wiley & Sons.
- Homans G.C. (1951). The Human Group, London: Routledge and Kegan Paul.
- Homans G.C. (1958). Social behavior as exchange, in American Journal of Sociology, 63: 597-606.
- Hughes A.L. (1988). Evolution and Human Kinship, New York: Oxford University Press.
- Johnson S.B. & Johnson R.C. (1991). Support and conflict of kinsmen in Norse Earldoms, Icelandic families and English royalty, in Ethology and Sociobiology, 12: 211-220.
- Kana'Iaupuni S.M., Donato K.M., Thompson-Colon T. & Stainback M. (2005). Counting on kin: Social networks, social support, and child health status, in Social Forces, 83: 1137-1164.
- Keyfitz N. (1977). Applied mathematical demography, New York: Wiley.
- Kruger D.J. (2001). Psychological aspects of adaptations for kin directed altruistic helping behaviours, in Social Behavior and Personality, 29: 323-330.
- Kurland J.A. (1980). Kin selection theory: A review and selective bibliography, in Ethology and Sociobiology, 1: 255-274.
- Loehlin J.C. (2004). Latent variable models: An introduction to factor, path, and structural equation analysis. Mahwah: Lawrence Erlbaum.
- Low B.S. (2000). Why Sex Matters, a Darwinian Look at Human Behavior, Princeton: Princeton University Press.
- Magarick R.H. & Brown R.A. (1981). Social and emotional aspects of voluntary childlessness in vasectomized childless men, in Journal of Biosocial Science, 13: 157-167.
- Marsden P.V. (1987). Core Discussion Networks of Americans, in American Sociological Review, 52: 122–131.
- McAllister F. & Clarke L. (1998). Choosing Childlessness, London: Family Policy Studies Centre.
- McCullough J.M. & Barton E.Y. (1991). Relatedness and mortality risk during a crisis year: Plymouth Colony, 1620–1612, in Ethology and Sociobiology, 12: 195-209.
- McPherson M., Smith-Lovin J. & Cook J.M. (2001). Birds of a feather: Homophily in Social Networks, in Annual Review of Sociology, 27: 425-444.
- Menard S. (1995). Applied Logistic Analysis, Quantitative Applications in the Social Sciences Series #106, Thousand Oaks: Sage Publications.
- Michailidis G. & de Leeuw J. (1998). The Gifi System of Descriptive Multivariate Analysis, in Statistical Science, 13: 307-336.
- Miller R.J. & Darlington Y. (2002). Who supports? The providers of social support to dual-parent families caring for young children, in Journal of Community Psychology, 30: 461-475.
- Mirowsky J. & Ross C.E. (2002). Family relationships, social support and subjective life-expectancy, in Journal of Health and Social Behavior, 43: 469-489.
- Mock D.W. & Parker G.A. (1997). The evolution of sibling rivalry, Oxford: Oxford University Press.
- Mock D.W. & Parker G.A. (1998). Siblicide, family conflict and evolutionary limits of selfishness, in Animal Behaviour, 56: 1-10.
- Molm L.D. (1997). Coercive power in social exchange, Cambridge: Cambridge University Press.
- Morgan C. (1979). Eskimo Hunting Groups, Social Kinship and the Possibility of Kin Selection in Humans, in Ethology and Sociobiology, 1:83–91.
- Morgan S.P. & King R.B. (2001). Why Have Children in the 21st Century? Biological Predisposition, Social Coercion, Rational Choice, in European Journal of Population, 17: 3-20.
- Mosher W.D., Williams L.B. & Johnson. P.D. (1992). Religion and Fertility in the United States: New Patterns, in Demography, 29: 199–214.
- Muhuri P.K. & Preston S.H. (1991). Effects of Family Composition on Mortality Differentials by Sex Among Children in Matlab, Bangladesh, in Population and Development Review, 17: 415-434.
- Muhuri P.K. & Menken J. (1997). Adverse Effects of Next Birth, Gender, and Family Composition on Child Survival in Rural Bangladesh, in Population Studies, 51: 279-294.
- Nagelkerke N.J.D. (1991). A note on a general definition of the coefficient of determination, in Biometrika, 78: 691-692.
- Nelson M. (1998). Children by choice: the evolutionary implications of choosing childlessness, unpublished MSc.-Thesis, Liverpool: University of Liverpool.
- Neyer F.J. & Lang F.R. (2003). Blood is thicker than water: kinship orientation across adulthood, in Journal of Personality and Social Psychology, 82: 310-321.
- NIDI (1997) (online). Bevolking van Nederland anno 1997 (‘The Population of the Netherlands at 1997’), in Demos, http://www.nidi.knaw.nl/web/html/public/demos/dm97071.html (consulted on 21-06-2005).
- NIDI (2004) (online). Demodata, in Demos, http://www.nidi.knaw.nl/web/html/public/demos/dm0405.pdf (consulted on 23-06-2005).
- O’Connor R.J. (1978). Brood reduction in birds, selection for infanticide, fratricide, suicide? in Animal Behaviour, 26: 79-96.
- Oates K. & Wilson M.I. (2002). Nominal kinship cues facilitate altruism, in Proceedings of the Royal Society London B, 269: 105-109.
- Olson M. (1965). The logic of collective action: public goods and the theory of groups, Cambridge: Harvard University Press.
- Pampel F. C. (2000). Logistic regression: A primer, Quantitative Applications in the Social Sciences Series #132, Thousand Oaks: Sage Publications.
- Park K. (2002). Stigma management among the voluntarily childless, in Sociological Perspectives, 45: 21-45.
- Park K. (2005). Choosing Childlessness: Weber’s Typology of Action and Motives of the Voluntarily Childless, in Sociological Inquiry, 75: 372-402.
- Peng C.-Y.J., Lee K.L. & Ingersoll G. (2002). An Introduction to Logistic Regression Analysis and Reporting, in Journal of Educational Research, 96: 1-14.
- Pearce D., Cantisani G., Laihonen A. (1999) (online). Changes in fertility and family sizes in Europe, in Population Trends, http://www.statistics.gov.uk/downloads/theme_population/PT95_v2.pdf (consulted on 21-06-2005).
- Phillipson C. (1997). Social relationships in later life: A review of the research literature, in International Journal of Geriatric Psychiatry, 12: 505-512.
- Plug W., Zeijl E. & Du Bois-Reymond M. (2003). Young People’s Perceptions on Youth and Adulthood A Longitudinal Study from The Netherlands, in Journal of Youth Studies, 6: 127-144.
- Ruddock V., Wood R. & Quinn M. (1998) (online). Birth statistics: recent trends in England and Wales, in Population Trends, http://www.statistics.gov.uk/articles/population_trends/birthstats_pt94.pdf (consulted on 21-06-2005).
- Sear R., Mace R. & McGregor I.A. (2000). Maternal grandmothers improve nutritional status and survival of children in rural Gambia, in Proceedings of the Royal Society London B, 267: 1641-1647.
- Sear R., Steele F., McGregor I.A. & Mace R. (2002). The effects of kin on child mortality in rural Gambia, in Demography, 39: 43-63.
- Shaanker U., Ghaneshaiah K.N. & Bawa K.S. (1988). Parent-offspring conflict, sibling rivalry and brood size patterns in plants, in Annual Review of Ecology and Systematics, 19: 177-205.
- Sigman M., Neumann C., Carter E., Cattle D., D’Souza S. & Bwibo N. (1988). Home Interactions and the Development of Embu Toddlers in Kenya, in Child Development, 59: 1251-1261.
- Social Trends 30 (2000). London: Central Statistical Office.
- Social Trends 34 (2004). London: Central Statistical Office.
- Somers M.D. (1993). A Comparison of Voluntarily Childfree Adults and Parents, in Journal of Marriage and the Family, 55: 643-650.
- SPSS (2001). SPSS Categories 11, Chicago: SPSS.
- Sulloway F. (1996). Born to rebel, New York: Pantheon.
- Sulloway F. (2001). Birth order, sibling competition, and human behavior, in Davies P.S. & Holcomb H.R. (eds.) (2001). Conceptual Challenges in Evolutionary Psychology: Innovative Research Strategies, Dordrecht: Kluwer Academic Publishers, 39-83.
- Turke P.W. (1988). Helpers at the nest: childcare networks on Ifaluk, in Betzig L., Borgerhoff-Mulder M. & Turke P.W. (eds.) (1998). Human Reproductive Behaviour, Cambridge: Cambridge University Press, 178-188.
- Turke P.W. (1989). Evolution and the demand for children, in Population and Development Review, 15: 61-90.
- Turner H.A & Turner R.J. (1999). Gender, social status and emotional reliance, in Journal of Health and Social Behavior, 40: 360-373.
- Turner R.J. & Marino F. (1994). Social support and social structure: A descriptive epidemiology, in Journal of Health and Social Behavior, 35: 193-212.
- van de Kaa D.J. (1996). Anchored narratives: The story and findings of half a century of research into the determinants of fertility, in Population Studies, 50: 389-432.
- van de Kaa D.J. (2004). The true commonality: In reflexive modern societies fertility is a derivative, in Population Studies, 58: 77-81.
- Wang X. (1996). Evolutionary hypotheses of risk sensitive choice, in Ethology and Sociobiology, 17: 1-15.
- Weisner T.S. & Gallimore R. (1977). My Brother’s Keeper: Child and Sibling Caretaking, in Current Anthropology, 18: 169-190.
- Wenger G.C. (1992). Help in old age: facing up to change: a longitudinal network study, Liverpool: Liverpool University Press.
- Wenger G.C. (1997). Review of findings on support networks of older Europeans, in Journal of Cross-Cultural Gerontology, 12: 1-21.
- Wenger G.C., Scott A. & Patterson N. (2000). How important is parenthood? Childlessness and support in old age in England, in Aging and Society, 20: 161-182.
- Wilson E.O. (2000[1975]). Sociobiology: The New Synthesis, Cambridge: the Belknap press of the Harvard University press.
- Zanting A., Verloop N. & Vermunt J.D. (2001). Student teachers’ beliefs about mentoring and learning to teach during teaching practice, in British Journal of Educational Psychology, 71: 57-80.
- Zhou W.-X., Sornette D., Hill R.A. & Dunbar R.I.M. (2005). Discrete hierarchical organization of social group sizes, in Proceedings of the Royal Society London B, 272: 439-444.
| home | list theses | contence | previous | next |
[1] see van de Kaa (1996) for a thorough review of explanations for fertility transitions.
[2] However, this ‘new’ freedom of choice is of course not ‘real freedom’. Individual choices are governed and structured by ‘new’ institutions and ‘new’ rules (Beck & Beck-Gernsheim 2002; Beck-Gernsheim, 2002).
[3] For the UK, it is estimated that as many as 25 percent of the women born in 1973 will remain childless (Social Trends 30, 2000). It is expected that this trend will further continue (Social Trends 34, 2004).
[4] Interestingly, Kana'Iaupuni and colleagues (2005) found that extended kin, rather than immediate kin, improved child health status amongst deprived families in Mexico.
[5] Yet, it could also be the other way around individuals are willing to incur high costs because they are in high quality relationships. Either way, high ‘costs’ and strong relationships appear to go together.
[6] However, genetic relatedness could but does not necessarily affect initiative of contact or financial balance as relatedness affects both siblings.
[7] In addition, as a separate study, using a different data-set, we have investigated whether or not childless individuals ‘invest’ more and have higher quality relationships with their nephews/nieces than ‘parents’. Due to considerations of space the entire study can be found in the cd-rom. This study is not central to the Msc.-thesis and we will not thoroughly discuss it in the core text.
[8] It is important to bear in mind that this question is only asked to men of age 50 or younger, women of age 45.
[9] It was not possible to get a closer estimate
[10] See below why we chose two categories instead of three categories.
[11] Yet, it is important to bear in mind that we are working with a very large sample size.
[12] For examples of research with HOMALS see Zanting et al., 2001 and Plug et al., 2003. Statistics for the HOMALS presented here can be found on the cd-rom.
[13] Dimensions in HOMALS load on several variables/categories, therefore it is difficult to label these dimensions.
[14] SPSS was unable to calculate the full model in the backward stepwise procedure. However, if we left out age difference, the backward stepwise procedure selects the same variables. (Previous models with less variables showed no differences in selected variables between parameter selection procedures).
[15] We are interested in level of ‘significance’ rather than effect size for these variables, as it is ‘significance’ level that determines whether a parameter gets selected in the multinomial logistic regression. Therefore we used χ² instead of other statistical measures.
[16] Yet, if we use a one-tailed test, the difference is significant. An alternative statistical measure is significant for both variables: Interest given: Somers’ Dyx= 0,117; p=0,039; interest received: Somers’ Dyx= 0,171; p= 0,001.
[17] Interestingly, individuals are also significantly more likely to receive advice, which was surveyed in the same way as interest, from a full sibling than from an adopted or half-sibling (Somers’ Dyx= 0,157; p<0,001). Yet genetic relatedness does not appear to influence giving advice (Somers’ Dyx= 0,054; p=0,253).
[18] Proportions are for each category according to genetic status (and not for total siblings).
[19] Also note that some variables, e.g. sex of the respondent, selected in the regression above are not selected in the model here. Inclusion of education, living siblings or interest received shows models with no independent effect for genetic relatedness.
[20] With 95% confidence, we can state that full siblings are between 1,21 and 6,24 more likely than adopted or half-siblings to have a very good relationship versus a not great relationship with their sibling. Also, full siblings are between 1,29 and 4,89 times more likely than adopted or half-siblings to have a good relationship versus a not great relationship with their sibling. (Both while controlling for other variables in the model). Note that childlessness is not significant for certain parameter estimates as the reference category is ‘not great’.
[21] The NKPS data set contains data on the sibling’s evaluation of the relationship with the respondent as well. There is some indication that childless siblings are not significantly closer related to their ‘anchor’ (see cd-rom). Yet, sample size is small compared to base sample (n= 936 versus n= 4710). How this can be reconciled with the highly significant finding in the base sample is unclear. We believe this might be due to the survey method: computer assisted personal interview versus mail survey.
[22] No interaction effects with education were constructed as the algorithm (in SPSS) encounters numerical problems.
[23] In certain cases, it is possible that an interaction-term is significant, without one of the main effects being significant.
[24] As it is a very strong predictor it is likely to obscure (independent) effects of other variables, as argued before (see also Figure 2 and Figure 3).
[25]1,45 times more likely for siblings with children corresponds to (0,69)-1 (times for childless siblings).
[26] We should bear in mind however that sample size is large.
[27] We should bear in mind however that sample size is large.
[28] We change the reference category because the differences between childless individuals and parents lie between different categories than for genetic relatedness as can be read from the graphs presented. The model characteristics, e.g. model χ² or Nagelkerke R², remain the same.
[29] 2,11 less likely equals 1/0,47 more likely.
[30] Ideally, we would use income in euro’s as a predictor. Unfortunately, more than half of the sample has not answered to questions on income. This is problematic and therefore we will solely use ‘education’, which is generally a reliable proxy for income, as a predictive measure.
[31] It is possible to further distinguish according to the amount given, whether or not more than 500 euro’s was given (over the past twelve months). Yet, SPSS incurs numerical problems for these regressions. The (uncertain) estimates can be found on the cd-rom.
[32] Ideally, we would use income in euro’s as a predictor. Unfortunately, more than half of the sample has not answered to questions on income. This is problematic and therefore we will solely use ‘education’, which is generally a reliable proxy for income, as a predictive measure. It is possible to further distinguish according to the amount given, whether or not more than 500 euro’s was given (over the past twelve months). Yet, SPSS incurs numerical problems for these regressions. The (uncertain) estimates can be found on the cd-rom.
[33] Yet, for interest given (Mann-Whitney U= 3528; one-tailed p= 0,063) and initiative of contact (Mann-Whitney U= 3625,5; one-tailed p= 0,083) results are close to reaching five percent significance level (see cd-rom).
[34] It might be important to note that the questions on interest given and received were asked before the questions on financial balance
[35] Mann-Whitney U= 6624,5 ; one-tailed p= 0,31